Euclid's Elements facts for kids
.jpg)
Euclid's Elements is a very important set of math books about geometry. It was written by the ancient Greek mathematician named Euclid around 300 BC. He lived in Alexandria, Egypt.
The Elements has 13 parts, or volumes. These parts have often been printed as 13 separate books (numbered I-XIII). It has been translated into many languages, including Latin, where it was called "Euclidis Elementorum". It is the most famous math book from ancient times.
Euclid gathered all the geometry knowledge of his time. His Elements is the main source of ancient geometry. Textbooks based on Euclid's work are still used today. In the book, Euclid starts with a few basic ideas called axioms. These are things that everyone agrees are true without needing proof. From these axioms, Euclid then shows how geometric shapes and whole numbers work.
The Elements also talks about perspective, conic sections (like circles and ellipses), and geometry on spheres. Besides geometry, it includes number theory. Euclid also came up with the idea of greatest common divisors. The greatest common divisor of two numbers is the biggest number that can divide evenly into both of them.
For a long time, the geometry in Elements was simply called "geometry." People thought it was the only kind of geometry possible. Today, we call it Euclidean geometry. This helps us tell it apart from other types of geometry, called non-Euclidean geometries, which mathematicians found in the 19th century.
About the Books
Euclid's Elements is made up of 13 books. Each book focuses on different parts of geometry and number theory.
- Books 1-4: These books cover basic plane geometry. This includes things like triangles, parallel lines, and circles.
- Books 5-6: These deal with ratios and proportions. They show how to compare sizes of different shapes.
- Books 7-10: These books are about number theory. They discuss prime numbers, how numbers divide each other, and irrational numbers.
- Books 11-13: These last books focus on solid geometry. They describe 3D shapes like cubes, pyramids, and spheres.
Euclid's way of thinking, starting with simple truths and building up complex ideas, has influenced science and math for thousands of years.
Important Translations
Euclid's Elements has been translated into many languages over the centuries. This helped spread his ideas around the world.
- Latin: One of the first important translations was into Latin. This made the book available to scholars in Europe.
- Arabic: Arabic scholars also translated Euclid's work. They helped keep his ideas alive during the Middle Ages.
- English: The first English version was published by Henry Billingsley in 1570.
- Chinese: In 1607, Matteo Ricci and Xu Guangqi published a Chinese edition. This brought Euclid's geometry to China.
These translations show how important Euclid's work was to many different cultures and times.
Images for kids
-
A fragment of Euclid's Elements on part of the Oxyrhynchus papyri.
-
A double-page from the Ishaq ibn Hunayn's Arabic Translation of Elementa from Iraq, 1270.
-
An image from a manuscript based on Adelard of Bath's translation of the Elements, around 1309–1316.
-
A page with notes from the first printed edition of Elements, printed by Erhard Ratdolt in 1482.
-
An animation showing how Euclid constructed a hexagon (Book IV, Proposition 15).
-
Codex Vaticanus 190.
-
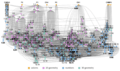
Propositions plotted with lines connected from Axioms on the top and other preceding propositions, labelled by book.
-
Proof of the Pythagorean theorem in Byrne's The Elements of Euclid published in 1847.
.jpg)
See also
In Spanish: Elementos de Euclides para niños
