Sum facts for kids
The sum of two or more numbers is what you get when you add them all together. This math operation is called summation. Think of it like counting how many items you have in total.
For example, if you have 2 apples, 4 bananas, and 6 oranges, the sum of your fruits is 2 + 4 + 6 = 12.
Contents
What is Sigma Notation?
Sigma notation is a special way to write long addition problems in a short, neat form. It uses the Greek letter Sigma (which looks like a big "E": 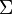 ).
).
This notation helps mathematicians and scientists write down sums that have many numbers, sometimes even an endless amount!
Here's how it works:
- The
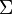 symbol means "add everything up."
symbol means "add everything up." - Below the
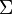 , you'll see something like "
, you'll see something like "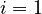 ". This tells you where to start counting. The letter i (or sometimes j or k) is called the index. It's like a counter.
". This tells you where to start counting. The letter i (or sometimes j or k) is called the index. It's like a counter. - Above the
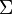 , you'll see a number. This tells you where to stop counting.
, you'll see a number. This tells you where to stop counting. - Next to the
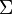 , you'll see a rule or formula, like "
, you'll see a rule or formula, like "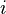 " or "
" or "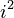 ". This tells you what numbers to add.
". This tells you what numbers to add.
Let's look at an example: 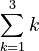 This means:
This means:
- Start with
 .
. - Add the value of
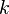 .
. - Increase
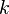 by 1.
by 1. - Keep going until
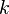 reaches 3.
reaches 3.
So, 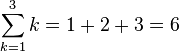 .
.
Basic Rules for Sums
Sums follow some simple rules. Here are a few examples to help you understand:
- If you add zero many times, the sum is always zero:
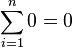
- If you add the number 1 a certain number of times (let's say n times), the sum will be n:
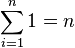 For example,
For example, 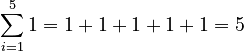 .
.
- If you add the same number n a certain number of times (let's say n times), the sum will be n multiplied by n, which is n squared:
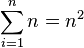 For example,
For example, 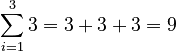 , which is
, which is 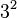 .
.
Where Are Sums Used?
Sums are super useful in many areas of math and science. They help us understand patterns and sequences of numbers.
Series and Sequences
Sums are used to represent series and sequences. A sequence is a list of numbers in a specific order, and a series is the sum of the numbers in a sequence.
For example, imagine a sequence where each number is half of the previous one: 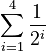 This means we add the first four numbers in this sequence:
This means we add the first four numbers in this sequence: 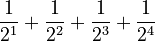 Which is:
Which is: 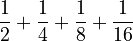
Repeating Decimals
Sums can even help us understand repeating decimals! A repeating decimal is a number like 0.3333... where a digit or group of digits repeats forever.
For example, the repeating decimal 0.3333... can be written as a sum: 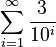 This means:
This means: 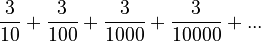 If you add all these numbers together, you get exactly
If you add all these numbers together, you get exactly  !
!
Related Pages

