Sequence facts for kids
A sequence is a list of things that follow each other in a special order. Think of it like a line of numbers, colors, or events where the order really matters. For example, (Blue, Red, Yellow) is a sequence, and it's different from (Yellow, Blue, Red) because the order changed.
In mathematics, sequences are very important. When a sequence is made of numbers, it's often called a progression.
Sequences can be either finite or infinite.
- A finite sequence has a clear end. For example, (1, 2, 3, 4, 5) is a finite sequence because it stops at 5.
- An infinite sequence keeps going forever and never ends. The sequence of all even numbers greater than 0 (2, 4, 6, 8, ...) is an infinite sequence because you can always find another even number.
For infinite sequences, we can't just write down every single item. Instead, we use a rule to describe them. This rule tells us how to find any item in the sequence, no matter how far along it is. We often use the letter n to stand for the position of an item in the sequence (like 1st, 2nd, 3rd, and so on). We might write a sequence as 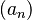 , where
, where 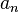 means "the item in the n-th spot."
means "the item in the n-th spot."
For example, imagine a rule where the item in the n-th spot is found by multiplying 2 by n (2×n).
- The first item (where n=1) is 2×1 = 2.
- The second item (where n=2) is 2×2 = 4.
- If you want the 100th item (where n=100), you just calculate 2×100 = 200.
This rule lets us find any item in the sequence, even if it goes on forever!
Contents
Kinds of Sequences
Arithmetic Progressions
An arithmetic progression (often called an AP) is a sequence where the difference between any item and the one right before it is always the same. This constant difference is called the "common difference."
Let's look at an example: 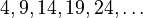
- 9 minus 4 equals 5.
- 14 minus 9 equals 5.
- 19 minus 14 equals 5.
The common difference here is 5.
If the first item in the sequence is a and the common difference is D, you can find any item in the sequence using this rule: 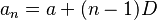 Here,
Here, 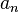 is the item in the n-th position.
is the item in the n-th position.
Geometric Progressions
A geometric progression (or GP) is a sequence where the ratio (what you multiply by) between any item and the one right before it is always the same. This constant ratio is called the "common ratio."
Here's an example: 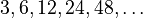
- 6 divided by 3 equals 2.
- 12 divided by 6 equals 2.
- 24 divided by 12 equals 2.
The common ratio here is 2.
If the first item is a and the common ratio is r, you can find any item using this rule: 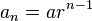 Again,
Again, 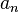 is the item in the n-th position.
is the item in the n-th position.
Harmonic Progressions
A harmonic progression (HP) is a special kind of sequence. If you take the reciprocal (1 divided by the number) of each item in a harmonic progression, those new numbers will form an arithmetic progression.
Example: 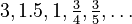 Let's find the reciprocals:
Let's find the reciprocals:
- Reciprocal of 3 is
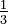 .
. - Reciprocal of 1.5 is
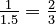 .
. - Reciprocal of 1 is
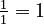 .
. - Reciprocal of
 is
is 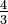 .
.
The sequence of reciprocals is 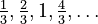 . Notice that the difference between these reciprocal terms is always
. Notice that the difference between these reciprocal terms is always 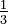 (e.g.,
(e.g., 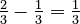 ,
, 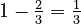 ). This means the reciprocals form an arithmetic progression.
). This means the reciprocals form an arithmetic progression.
Series
A series is what you get when you add up all the items in a sequence.
For an arithmetic sequence, if you want to find the sum (S) of the first n items, you can use this rule: ![S=\frac{n}{2}[2a+(n-1)d]](/images/math/c/3/3/c3333eb78dc2d83ffd022a3edf1b9158.png) Here, a is the first item, d is the common difference, and n is how many items you are adding up.
Here, a is the first item, d is the common difference, and n is how many items you are adding up.
For a geometric sequence, the sum (S) depends on whether it's finite or infinite:
- If the sequence is finite (it ends), the sum of the first n items is:
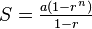
- If the sequence is infinite (it goes on forever) and the common ratio r is between -1 and 1 (not including -1 or 1), the sum is:
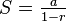 In these rules, a is the first item, r is the common ratio, and n is the number of items (for finite sequences).
In these rules, a is the first item, r is the common ratio, and n is the number of items (for finite sequences).
Related pages
See also
 In Spanish: Sucesión (matemática) para niños
In Spanish: Sucesión (matemática) para niños

