Cauchy sequence facts for kids
In mathematics, a Cauchy sequence is a special kind of sequence (a list of numbers in order). In a Cauchy sequence, the numbers in the list get closer and closer to each other as you go further along the list.
Imagine you have a list of numbers, like 1, 0.5, 0.25, 0.125, and so on. As you move along this list, the numbers get closer and closer to zero. A Cauchy sequence is like this, but instead of just getting closer to one specific number, the numbers in the list also get closer to each other.
Cauchy sequences are named after a famous French mathematician named Augustin-Louis Cauchy.
What is a Cauchy Sequence?
A sequence is just an ordered list of numbers. For example, 1, 2, 3, 4, ... is a sequence. Another one is 1, 1/2, 1/3, 1/4, ...
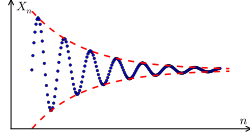
A sequence is "Cauchy" if, as you go further and further along the list, the numbers become extremely close to each other. No matter how tiny a distance you pick, eventually all the numbers in the sequence will be within that tiny distance of each other.
Think of it like a group of friends walking towards a meeting point. As they get closer to the meeting point, they also get closer to each other. A Cauchy sequence is like this group of friends, where the numbers in the sequence are the friends.
Getting Closer and Closer
Let's look at an example. Consider the sequence:
- 1, 0.5, 0.25, 0.125, 0.0625, ... (each number is half of the previous one)
If you pick any two numbers far along in this sequence, they will be very close to each other. For instance, the 10th number and the 11th number will be much closer than the 1st and 2nd numbers. This sequence is a Cauchy sequence because its numbers are getting closer and closer to zero, and also closer and closer to each other.
Not all sequences are Cauchy. For example, the sequence 1, 2, 3, 4, ... is not Cauchy. The numbers keep getting further apart, not closer.
Why are They Important?
Cauchy sequences are very important in advanced mathematics. They help mathematicians understand if a sequence is "converging." A sequence "converges" if its numbers get closer and closer to a single, specific number. This specific number is called the "limit" of the sequence.
For example, the sequence 1, 0.5, 0.25, ... converges to 0. The number 0 is its limit.
In many mathematical spaces (like the usual number line), if a sequence is Cauchy, it means it *must* converge to a limit. This is a very powerful idea. It means if the numbers in a sequence are getting closer and closer to each other, they are definitely heading towards a specific destination.
This idea helps mathematicians define and understand "complete" spaces. A space is "complete" if every Cauchy sequence in that space has a limit that is also in that space. The set of all real numbers (all numbers on the number line, including decimals and fractions) is a complete space.
