Limit of a sequence facts for kids

The plot of a convergent sequence {a_n} is shown in blue. Visually we can see that the sequence is converging to the limit 0 as n increases.

This picture shows a Cauchy sequence (x_n). You can see the terms of the sequence getting closer and closer to each other as n gets bigger. In real numbers, every Cauchy sequence gets closer to some limit.

In mathematics, a sequence is like an ordered list of numbers or other mathematical objects. Imagine counting: 1, 2, 3, 4... that's a sequence. Or even numbers: 2, 4, 6, 8...

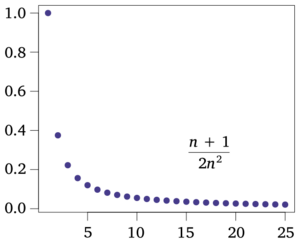
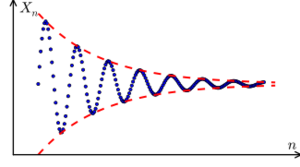
Sometimes, the numbers in a sequence get closer and closer to a certain value. This value is called the limit of the sequence. When a sequence has a limit, we say it is convergent. If it doesn't get closer to a single value, it's called divergent.

When a sequence is convergent, the difference between the current number in the sequence and the limit gets smaller and smaller, almost reaching zero, as you go further along the sequence.

What Does "Getting Close" Mean?

When we say a sequence gets "closer and closer" to a limit, it means something very specific in math. Imagine you pick a tiny distance, let's call it "epsilon" (a Greek letter written as ). This epsilon can be super, super small, like 0.000001.

For a sequence to have a limit, no matter how tiny you make that epsilon, you can always find a point in the sequence after which all the following numbers in the sequence are within that tiny distance from the limit. They never stray further away.

We write this idea like this: or 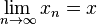. This means "the sequence 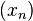approaches the limit as gets very large."

If a sequence reaches a limit, it's convergent. If it doesn't, it's divergent.

A Brief History of Limits

The idea of things getting "infinitely close" has been around for a very long time!

• The ancient Greek philosopher Zeno of Elea created famous puzzles that involved ideas similar to limits. For example, his paradox about Achilles and the tortoise makes you think about how you can cover an infinite number of smaller and smaller distances.
• Later, Greek mathematicians like Eudoxus and Archimedes used a method called the "method of exhaustion." They would use an infinite series of shapes that got closer and closer to the area or volume of a curved shape. This helped them find the exact area or volume. Archimedes even figured out how to sum what we now call a geometric series.

• In the 17th century, Isaac Newton worked with series in his studies. He used the idea of "taking the limits" when a value got very, very close to zero. This was important for developing calculus.

• During the 18th century, mathematicians like Euler were very good at calculating sums of series, even if they didn't always worry if a true "limit" existed.

• However, by the end of that century, Lagrange felt that mathematics needed to be more strict and precise.

• The first time someone really looked at the conditions for a series to converge to a limit in a strict way was Carl Friedrich Gauss in 1813.

• The modern, very precise definition of a limit (the one with the "epsilon" idea) was developed by Bernhard Bolzano in 1816 and later by Karl Weierstraß in the 1870s. This strict definition helped make calculus and other areas of mathematics much stronger.

Related pages

• Limit of a function

See also

In Spanish: Límite de una sucesión para niños