Limit of a function facts for kids

In calculus, a part of mathematics, the limit of a function helps us understand what a function is doing very close to a certain number. It's like looking at what happens to a path as you get super close to a specific spot, even if you can't actually stand on that spot. Limits are a key idea in calculus, along with derivatives and integration.

What is a Limit?

Imagine you have a machine (a function) that takes a number (let's call it x) and gives you another number (let's call it f(x)). A limit tells us what number f(x) gets very, very close to as x gets very, very close to some specific number.

We write this using a special math symbol: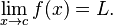

This means "The limit of f(x) as x gets close to c is L." It tells us that as x gets super close to c (but not exactly c), the value of f(x) gets super close to L.

An Example of a Limit

Let's look at the function 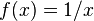. This function means you take a number x and divide 1 by it.

What happens if x is 0? You can't divide by zero! So, 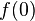is undefined. On a graph, this function would have a gap or a "wall" at x = 0. This wall is called a vertical asymptote.

Even though we can't use x = 0, we can see what happens as x gets very close to 0.

• If x is a tiny positive number (like 0.0000001), then 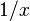becomes a very large positive number.
• If x is a tiny negative number (like -0.0000001), then 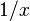becomes a very large negative number.

In limit language, we say: The limit of 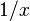as approache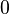s is 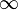(infinity). We write this as: 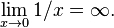This means the function's value keeps growing bigger and bigger as x gets closer to 0.

Limits from the Right and Left

Sometimes, a function acts differently depending on which side you approach a number from.

• The left limit is when x gets close to a number from values smaller than it. For example, approaching 0 from -1, -0.5, -0.1.
• The right limit is when x gets close to a number from values larger than it. For example, approaching 0 from 1, 0.5, 0.1.

For the function :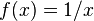

• As x approaches 0 from the right (like 0.1, 0.01, 0.001), 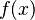goes towards positive infinity.
• As x approaches 0 from the left (like -0.1, -0.01, -0.001), 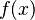goes towards negative infinity.

For a limit to exist at a point, the left limit and the right limit must be the same. Since they are different for 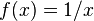at 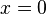, we say the overall limit does not exist there.

Related pages

• Derivative (mathematics), a quantity defined as a limit of slopes
• Limit of a sequence

See also

In Spanish: Límite de una función para niños