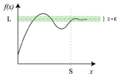
Limit (mathematics) facts for kids
In mathematics, a limit helps us understand what value a function or a sequence is getting very, very close to. Imagine you're walking towards a spot, but you can never quite step on it. A limit tells us exactly where that spot is.
Sometimes, when we do math operations, especially when drawing graphs, certain numbers can cause problems. For example, you can't divide by zero! Limits help us explain what happens around these tricky points, showing us the "expected" value even if the function itself can't reach it.
Contents
Understanding Limits: What They Are
Limits are super important in a part of math called calculus. They help us define big ideas like continuity (if a graph can be drawn without lifting your pencil), derivatives (how fast something is changing), and integrals (finding the total amount or area).
How We Write Limits
When we talk about limits for a function f, we write it like this: 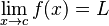 This means "the limit of f of x, as x gets closer and closer to c, is L".
This means "the limit of f of x, as x gets closer and closer to c, is L".
Another way to say it is "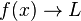 as
as  ". This just means "
". This just means "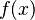 tends towards
tends towards 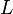 as
as  tends towards
tends towards  ". We shorten "limit" to lim.
". We shorten "limit" to lim.
For a sequence (a list of numbers in order), we use a similar idea: 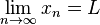 This means as n (the position in the sequence) gets super big, the numbers in the sequence
This means as n (the position in the sequence) gets super big, the numbers in the sequence 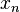 get closer to L.
get closer to L.
Exploring Limits with an Example
Let's look at an example. Imagine a function where you give it a number,  , and it gives you back
, and it gives you back  . We call the output
. We call the output  . If we plot these points on a graph, it looks interesting!
. If we plot these points on a graph, it looks interesting!
Here's what happens with some numbers:
| x input | function | y output | x, y (coordinates) |
|---|---|---|---|
| 4 | 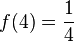 |
0.25 | 4, 0.25 |
| 3 | 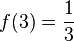 |
0.33 | 3, 0.33 |
| 2 | 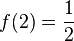 |
0.5 | 2, 0.5 |
| 1 | 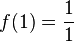 |
1 | 1, 1 |
| 0 | 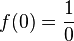 |
undefined | 0, undefined |
As you can see, if we try to put in 0, we get "undefined" because you can't divide by zero.
Getting Closer to the Limit
Even though we can't use 0, we can see what happens as we get super close to 0. Look at these numbers:
| x input | function | y output | x, y (coordinates) |
|---|---|---|---|
| 1 | 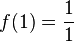 |
1 | 1, 1 |
| 0.5 | 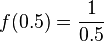 |
2 | 0.5, 2 |
| 0.25 | 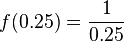 |
4 | 0.25, 4 |
| 0.125 | 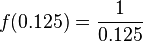 |
8 | 0.125, 8 |
| -0.125 | 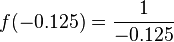 |
-8 | -0.125, -8 |
| -0.25 | 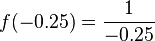 |
-4 | -0.25, -4 |
| -0.5 | 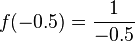 |
-2 | -0.5, -2 |
| -1 | 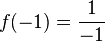 |
-1 | -1, -1 |
Notice that as x gets smaller and smaller (closer to 0), the output y gets bigger and bigger. If x is a tiny positive number, y becomes a huge positive number. If x is a tiny negative number, y becomes a huge negative number.
We describe this by saying: "The limit of 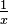 as
as  approaches 0 from the right side is
approaches 0 from the right side is 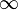 (infinity)". This means
(infinity)". This means 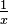 can keep growing without any upper limit, as long as x doesn't actually hit 0. We write this as:
can keep growing without any upper limit, as long as x doesn't actually hit 0. We write this as: 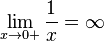 .
.
Real-World Uses of Limits
Even though a limit is a value that a function or sequence gets close to but might not actually reach, it's super useful for finding very accurate answers.
For example, the special mathematical constant called  (Euler's number) can be found using limits. We use the formula
(Euler's number) can be found using limits. We use the formula 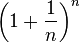 , where n is a number we choose:
, where n is a number we choose:
| n input | function | output (getting closer to e) |
|---|---|---|
| 1 | 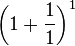 |
2 |
| 10 | 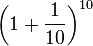 |
2.5937424601 |
| 10,000 | 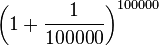 |
2.7182682372 |
| 10,000,000 | 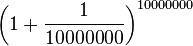 |
2.71828169398... |
As you can see, the bigger n gets, the closer the output gets to the actual value of  (which is about 2.71828). The equation will never be exactly equal to
(which is about 2.71828). The equation will never be exactly equal to  , but by making n larger, we get a much more accurate answer.
, but by making n larger, we get a much more accurate answer.
Mathematically, we say: "The limit of 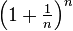 as n approaches
as n approaches 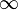 (infinity) is
(infinity) is  ". This is written as
". This is written as 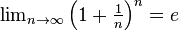 .
.
Related Math Topics
- Limit of a sequence
- Cauchy sequence
- Limit of a function
- Big O notation: This is used to describe how a function behaves when its input gets very large or very small.
Images for kids
See also
 In Spanish: Límite (matemática) para niños
In Spanish: Límite (matemática) para niños


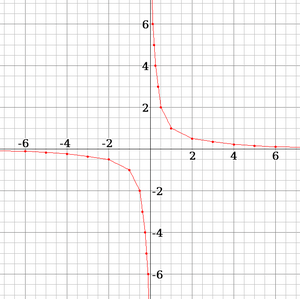
 . Notice how the line gets very close to the axes but never touches 0.
. Notice how the line gets very close to the axes but never touches 0.