Big O notation facts for kids
Big O notation is a way to describe how fast a computer program or "algorithm" works. It helps us compare different programs by looking at how much memory they need and how long they take to finish a task.
This notation is often used to figure out how difficult a problem is for a computer to solve. A mathematician named Paul Bachmann first used this idea in 1896. Later, Edmund Landau made it very popular, which is why it's sometimes called a "Landau symbol."
Big O notation gets its name from thinking about the "order of the function," which means how a program's time or memory use grows. It helps us find the upper bound (the highest possible amount) of this growth. This means it shows the longest time a program might take to turn an input into an output. So, programs can be grouped by how long they might take in the worst possible situation.
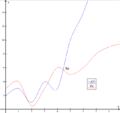
Big O helps us guess how long a program will run without actually running it on a computer. This is helpful because different computers have different parts, which can change how fast a program runs. Since Big O always assumes the worst case, it gives a steady way to measure speed. For example, a program that is  will always finish faster than one that is
will always finish faster than one that is 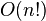 , no matter what computer you use.
, no matter what computer you use.
Contents
How Big O Works: Examples
Let's look at some examples using code written in Python. This isn't a full list of all Big O types, but it shows the main ideas.
Constant Time: O(1)
A program with  time always takes the same amount of time to run, no matter how big the input is.
time always takes the same amount of time to run, no matter how big the input is.
For example, imagine a function that takes a number (let's call it x) and just doubles it:
def double(x):
return x * 2 #Return the value of x times 2After getting the number, this function always takes just one step to give back the answer. It's "constant" because it always takes the same short time. So, it's an  program.
program.
Linear Time: O(n)
A program with 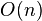 time takes longer to run as the size of the input, called
time takes longer to run as the size of the input, called  , gets bigger. The time it takes grows directly with the input size.
, gets bigger. The time it takes grows directly with the input size.
Look at this function that takes a number  and prints every number from 1 up to
and prints every number from 1 up to  :
:
def count(n):
i = 1 #Create a counter called "i" with a value of 1
while i <= n: #While i is less-than or equal to n
print(i) #Print the value of i
i = i + 1 #Redefine i as "the value of i + 1"If you give this function the number 5, it will print 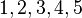 . This needs 5 loops to finish. If you give it 100, it will print
. This needs 5 loops to finish. If you give it 100, it will print 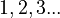 all the way to
all the way to 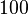 , needing 100 loops. If the input is
, needing 100 loops. If the input is  , the program will always do exactly
, the program will always do exactly  loops. That's why it's
loops. That's why it's 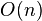 .
.
Factorial Time: O(n!)
A program with 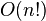 time takes a huge amount of time as the input grows. The time increases by a factorial amount, which means it gets very, very big, very fast.
time takes a huge amount of time as the input grows. The time increases by a factorial amount, which means it gets very, very big, very fast.
Let's say you want to visit five cities around the world and want to find every possible order you could visit them in. Here's a Python program that could do that:
import itertools #Import the itertools library
cities = ['London', 'Paris', 'Berlin', 'Amsterdam', 'Rome'] #An array of our chosen cities
def permutations(cities): #Taking an array of cities as input:
for i in itertools.permutations(cities): #For each permutation of our items (assigned to variable "i")
print(i) #Output iThis program finds and prints every unique way to order your cities. Some examples of what it might print are:
('London', 'Paris', 'Berlin', 'Amsterdam', 'Rome')
('London', 'Paris', 'Berlin', 'Rome', 'Amsterdam')
('London', 'Paris', 'Amsterdam', 'Berlin', 'Rome')
...
('Rome', 'Amsterdam', 'Paris', 'Berlin', 'London')
('Rome', 'Amsterdam', 'Berlin', 'London', 'Paris')
('Rome', 'Amsterdam', 'Berlin', 'Paris', 'London')
If you have 5 cities, the program will calculate 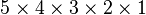 different orders. This is written as
different orders. This is written as 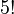 (5 factorial), which equals 120. If you had
(5 factorial), which equals 120. If you had  cities, it would find
cities, it would find 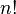 orders. Because it goes through every possible order, this program takes
orders. Because it goes through every possible order, this program takes 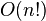 loops to finish.
loops to finish.
Little-o notation
There's a similar idea called little-o notation. Big-O says that a function doesn't grow faster than another function. Little-o says that a function grows more slowly than another function.
Think of it like comparing numbers:
- If
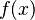 grows more slowly than
grows more slowly than 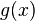 , then
, then 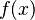 is both
is both 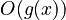 and
and 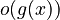 . This is like saying 3 is less than or equal to 5, and 3 is also less than 5.
. This is like saying 3 is less than or equal to 5, and 3 is also less than 5. - If
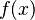 grows at the same speed as
grows at the same speed as 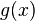 , then
, then 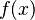 is
is 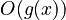 but not
but not 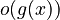 . This is like saying 5 is less than or equal to 5, but 5 is not less than 5.
. This is like saying 5 is less than or equal to 5, but 5 is not less than 5.
Related pages
- Time complexity
Images for kids
See also
 In Spanish: Cota superior asintótica para niños
In Spanish: Cota superior asintótica para niños