Factorial Facts for Kids

The factorial of a whole number n, written as n!, is found by multiplying n by all the whole numbers smaller than it, down to 1. For example, the factorial of 4 is 24, because 4 × 3 × 2 × 1 = 24. So, we can write 4! = 24.

For special math reasons, 0! is equal to 1.

What is Factorial?
The Story of Factorials
- Early Discoveries
- Factorials in Europe
Application
Related pages
Images for kids
See also

What is Factorial?

Factorial helps us figure out how many different ways we can arrange a certain number of items. Imagine you have a few different things, and you want to know all the possible orders you can put them in. Factorial is the tool for that!

Arranging Things with Factorial

Let's say you have three letters: A, B, and C. How many ways can you arrange them?

There are 6 different ways! Factorial shows us this:

For the first spot, you have 3 choices (A, B, or C).
For the second spot, you have 2 choices left.
For the last spot, you have only 1 choice left.

So, you multiply the choices: 3 × 2 × 1 = 6. This is the same as 3!.

How Factorial Grows

The factorial number grows very, very quickly! Even with a small number like 10, the factorial is huge.

10! = 3,628,800 ways to arrange 10 items.

Some Factorial Values
$n$	$n!$
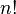0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	1.551121004×10²⁵
50	3.041409320×10⁶⁴
70	1.197857167×10¹⁰⁰
100	9.332621544×10¹⁵⁷
450	1.733368733×10¹⁰⁰⁰
1000	4.023872601×10²⁵⁶⁷
3249	6.412337688×10¹⁰⁰⁰⁰
10000	2.846259681×10³⁵⁶⁵⁹
25206	1.205703438×10¹⁰⁰⁰⁰⁰
100000	2.824229408×10⁴⁵⁶⁵⁷³
205023	2.503898932×10^1000004
1000000	8.263931688×10^5565708
10¹⁰⁰	10^{10^{101.9981097754820}}

Factorial and Recursion

Factorial is a great example of something called recursion. This is when a process repeats itself. You can write 3! as 3 × (2!). Then, 2! can be written as 2 × (1!). And 1! is 1 × (0!). Since 0! is 1, it stops there. So, n! can also be defined as n × (n-1)!, with 0! = 1. It's like a set of Russian nesting dolls, where each one helps define the next.

What Factorial is Not

The factorial function is not used for negative numbers. It only works for whole numbers that are zero or positive.

The Story of Factorials

The idea of factorials has been discovered by people in many different cultures throughout history.

Early Discoveries

In Indian mathematics, one of the first mentions of factorials was in ancient texts around 300 BCE to 400 CE. A Jain monk named Jinabhadra also described how to count arrangements in the 6th century. Later, around 1150, an Indian scholar named Bhāskara II used factorials to solve problems, like how many ways a god could hold different objects in their hands.

In the Middle East, a Hebrew book called Sefer Yetzirah (from 200 to 500 CE) listed factorials up to 7!. This was part of exploring how many words could be made from the Hebrew alphabet. An Arab mathematician named Ibn al-Haytham (around 965–1040 CE) was also one of the first to connect factorials with prime numbers.

Even though Greek mathematics had some ideas about counting, there's no clear proof they studied factorials directly. However, the Greek philosopher Plato famously suggested that an ideal community should have 5,040 people. This number is 7!, and it's special because it can be divided by many other numbers.

Factorials in Europe

In Europe, Jewish scholars first explored factorials by explaining the Sefer Yetzirah text. Later, in 1677, a British author named Fabian Stedman used factorials to describe "change ringing." This is a musical art where bells are rung in different patterns.

From the late 1400s, Western mathematicians started studying factorials more deeply. Luca Pacioli, an Italian mathematician, calculated factorials up to 11! in 1494 for a problem about arranging dining tables.

The special notation 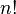$n!$ that we use today for factorials was introduced by a French mathematician named Christian Kramp in 1808. The word "factorial" itself was first used in 1800 by Louis François Antoine Arbogast.

Application

Factorials are used in many areas of mathematics, especially when we need to count different ways to arrange or choose things. They also pop up in computer science and probability theory.

Images for kids

Comparison of how factorials grow compared to other functions.
How accurate Stirling's formula is for estimating factorials.
A graph showing how the gamma function connects factorial values for non-whole numbers.
A 3D view of the gamma function, which extends factorials to complex numbers.