Bhāskara II facts for kids
Bhāskara II (around 1114–1185 AD) was a brilliant Indian mathematician and astronomer. People also called him Bhāskarāchārya, which means "Bhāskara, the teacher." He is known as Bhāskara II to avoid confusing him with an earlier mathematician named Bhāskara I.
Bhāskara II was born in 1114 AD in a place called Vijjadavida, in what is now Maharashtra, India. He came from a family of scholars who loved math and astronomy. His father, Maheśvara, taught him a lot about these subjects. Bhāskara II later became the head of an observatory in Ujjain, which was a major center for math and astronomy in ancient India.
His most famous work is called Siddhānta-Śiromaṇi, which means "Crown of Treatises." This big book is divided into four main parts, each like a separate book. These parts cover arithmetic, algebra, the math of planets, and spheres. He also wrote another book called Karaṇa-Kautūhala. Bhāskara II made huge contributions to math and astronomy in the 12th century and is often called the greatest mathematician of medieval India.
Quick facts for kids
Bhāskara II
|
|
|---|---|
| Born | c. 1114 AD Vijjadavida, Maharashtra
(Identified as Patan near Chalisgaon in present-day Khandesh or Beed in present-day Marathwada) |
| Died | c. 1185 AD |
| Other names | Bhāskarācārya |
| Era | Shaka era |
|
Notable work
|
Siddhānta Shiromani (Līlāvatī, Bījagaṇita, Grahagaṇita and Golādhyāya), Karaṇa-Kautūhala |
Contents
His Life and Family
Bhāskara II was born in 1114 AD. He finished his main book, Siddhānta-Śiromaṇi, when he was 36 years old, in 1150 AD. He also wrote another book, Karaṇa-kutūhala, when he was 69.
His family had a long history of being scholars, mathematicians, and astronomers. His great-great-great-grandfather and his father, Maheśvara, were also mathematicians. Bhāskara II taught his son, Lokasamudra, about math. Later, in 1207, Lokasamudra's son helped start a school to study Bhāskara's writings. Bhāskara II passed away in 1185 AD.
His Main Work: Siddhānta-Śiromaṇi
Bhāskara II's most important book, Siddhānta-Śiromaṇi, is like a big encyclopedia of math and astronomy. It has four main parts:
Līlāvatī (Arithmetic)
This first part is named after his daughter, Līlāvatī. It has 277 verses and teaches about basic math. It covers calculations, how numbers grow in patterns (progressions), measuring things, and how to arrange items in different ways.
Bījagaṇita (Algebra)
The second part, Bījagaṇita, has 213 verses. It talks about important math ideas like zero, infinity, and positive and negative numbers. It also shows how to solve different types of equations, including some very difficult ones that European mathematicians figured out centuries later.
Grahagaṇita (Planetary Math)
This third section, with 451 verses, focuses on the movement of planets. Bhāskara II looked at how fast planets move at any exact moment. He even had an idea similar to what we now call a "derivative" in calculus. He understood that a planet's speed is zero when it reaches its highest point in its orbit.
Amazing Math Discoveries
Bhāskara II made many important contributions to mathematics:
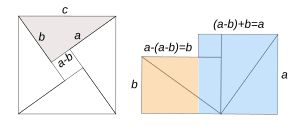
- He proved the Pythagorean theorem in a clever way. He calculated the area of a shape in two different ways and then showed how the theorem's formula (a² + b² = c²) comes out.
- He found ways to solve equations with powers of 2 (quadratic), 3 (cubic), and 4 (quartic).
- He solved equations where you need to find whole number solutions. This was called the Kuṭṭaka method. His rules were similar to what European mathematicians discovered much later.
- He developed a method called Chakravala to solve certain complex equations. This method was more advanced than what others used centuries later.
- He was the first to show that a positive number has two square roots: one positive and one negative.
- He worked with negative numbers and irrational numbers (numbers that can't be written as simple fractions).
- He had early ideas about calculus, a branch of math that deals with change. He understood concepts like instantaneous speed and how to find the maximum or minimum value of a function.
Arithmetic Skills
His book Līlāvatī is a detailed guide to arithmetic. It explains:
- What zero is and how to use it in calculations.
- How to multiply and find square numbers.
- How to calculate interest.
- How to solve equations where you need whole number answers. His methods were a big improvement on earlier ones.
Algebra Insights
His Bījagaṇita book was all about algebra. It covered:
- Positive and negative numbers.
- How to find unknown numbers in equations.
- Working with square roots of numbers that aren't perfect squares.
- Solving different types of equations, including those with more than one unknown.
Trigonometry Advances
Bhāskara II also knew a lot about trigonometry, which deals with triangles and angles. He created a table of sines (a trigonometric function) and understood how different trigonometric functions relate to each other. He also developed spherical trigonometry, which is used for calculations on the surface of a sphere, like the Earth.
Early Calculus Ideas
In his Siddhānta-Śiromaṇi, Bhāskara II showed early ideas related to calculus. He understood that when a changing quantity reaches its highest or lowest point, its rate of change becomes zero. This is a key idea in calculus. He also found a way to calculate the derivative of the sine function, even though he didn't use the modern term "derivative."
Astronomy Discoveries
Bhāskara II was also a great astronomer. He used earlier models to accurately figure out many things about space. For example, he calculated the length of a sidereal year (the time it takes for Earth to orbit the Sun) to be about 365.2588 days. This is very close to the modern measurement of 365.25636 days, a difference of only about 3.5 minutes!
His astronomy book, Siddhānta-Śiromaṇi, has two parts:
- The first part talks about the positions and movements of planets, lunar eclipses, and solar eclipses.
- The second part explains the nature of the sphere (like the Earth or celestial sphere), geography, and how to use astronomical instruments.
Engineering Ideas
Bhāskara II also had some interesting ideas in engineering. He described a wheel that he claimed could run forever, which is an early idea of a perpetual motion machine. He also used a measuring tool called Yaṣṭi-yantra to determine angles.
His Legacy
Bhāskara II's work has had a lasting impact. Many schools and institutes in India are named after him. In 1981, the Indian Space Research Organisation (ISRO) launched a satellite called Bhaskara II to honor him. There's even a documentary about him called Bhaskaracharya.
See also
 In Spanish: Bhaskara II para niños
In Spanish: Bhaskara II para niños
- List of Indian mathematicians