Permutation facts for kids
A permutation is a special way of arranging a group of things. Imagine you have a few toys, and you want to line them up. Each different way you can line them up is a permutation. Permutations are very useful in mathematics and in real life!
You can change one arrangement into another by simply switching two or more of the items. For example, if four friends are sitting in a car, the way they sit is a permutation. If they switch seats, it creates a different permutation.
Contents
What Are Permutations?
Permutations help us count how many different ways we can put things in order. Think about a lock with numbers. If the code is 1-2-3, that's one specific order. If you change it to 3-2-1, that's a different order, or a different permutation. The order matters a lot in permutations!
Why Order Matters
In permutations, the order of items is super important. Let's say you have three different colored blocks: red, blue, and green.
- Red, Blue, Green is one order.
- Green, Red, Blue is a different order.
- Blue, Green, Red is yet another order.
Each of these is a unique permutation because the order of the blocks is different.
Counting Permutations Without Repetition
When you arrange things and you can't use the same item more than once, we call it "permutations without repetition." This is where something called a factorial comes in handy!
Understanding Factorials
A factorial is a special math operation shown with an exclamation mark (!). For example, "3 factorial" is written as `3!`. To calculate it, you multiply all the whole numbers from 1 up to that number.
- `3! = 1 × 2 × 3 = 6`
- `4! = 1 × 2 × 3 × 4 = 24`
The number `n!` tells us exactly how many ways we can arrange `n` different things into a new order.
Example with Fruit
Let's say you have three different fruits: an orange, an apple, and a pear. How many different orders can you eat them in? Using the factorial, we can find out: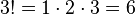 
This means there are 6 different ways to eat your fruit! Here are the ways:
- Orange, Apple, Pear
- Orange, Pear, Apple
- Apple, Orange, Pear
- Apple, Pear, Orange
- Pear, Orange, Apple
- Pear, Apple, Orange
As the number of items (`n`) gets bigger, the number of possible arrangements (permutations) grows very, very quickly!
See also
In Spanish: Permutación para niños
