Collatz conjecture facts for kids

German mathematician Lothar Collatz, who proposed the Collatz conjecture.

The Collatz conjecture is a super interesting idea in mathematics. It's like a puzzle that many smart people think is true, but no one has proven it yet! It's named after a German mathematician named Lothar Collatz. He first thought of this puzzle way back in 1937.

This puzzle is about what happens when you follow a simple set of rules, starting with any whole number. You keep doing the rules over and over again. The amazing thing is, no matter what number you start with, the Collatz conjecture says you will always end up at the number one!

How the Collatz Rules Work

The rules are quite simple. You pick a number, let's call it n. Then you do one of two things:

• If n is an even number (meaning you can divide it by two without anything left over), you just cut it in half. So, n becomes n divided by 2.
• If n is an odd number (meaning it can't be divided by two evenly), you multiply it by three and then add one. So, n becomes .

You keep applying these rules to the new number you get, until you reach the number one. The Collatz conjecture says this will always happen!

An Example: Starting with 9

Let's try an example to see how it works. We will start with the number 9:

• 9 (This number is odd, so we multiply by 3 and add 1: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 \times 9 + 1 = 27 + 1 = 28 )
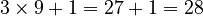• 28 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 28 \div 2 = 14 )
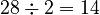• 14 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 14 \div 2 = 7 )
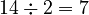• 7 (This number is odd, so we multiply by 3 and add 1: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 \times 7 + 1 = 21 + 1 = 22 )
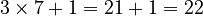• 22 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 22 \div 2 = 11 )
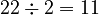• 11 (This number is odd, so we multiply by 3 and add 1: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 \times 11 + 1 = 33 + 1 = 34 )
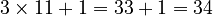• 34 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 34 \div 2 = 17 )
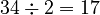• 17 (This number is odd, so we multiply by 3 and add 1: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 \times 17 + 1 = 51 + 1 = 52 )
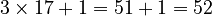• 52 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 52 \div 2 = 26 )
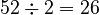• 26 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 26 \div 2 = 13 )
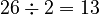• 13 (This number is odd, so we multiply by 3 and add 1: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 \times 13 + 1 = 39 + 1 = 40 )
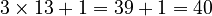• 40 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 40 \div 2 = 20 )
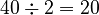• 20 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 20 \div 2 = 10 )
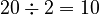• 10 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 10 \div 2 = 5 )
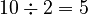• 5 (This number is odd, so we multiply by 3 and add 1: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3 \times 5 + 1 = 15 + 1 = 16 )
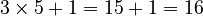• 16 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 16 \div 2 = 8 )
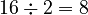• 8 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 8 \div 2 = 4 )
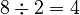• 4 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 4 \div 2 = 2 )
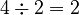• 2 (This number is even, so we divide it by 2: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 2 \div 2 = 1 )
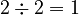• 1 (We reached 1! After 1, the sequence goes 4, 2, 1, and so on, in a loop.)

(oeis:A033479)

Why is it a Conjecture?

In mathematics, a "conjecture" is an idea that many smart people believe is true. They might have lots of evidence for it, like testing billions of numbers and seeing that the Collatz conjecture always holds true. However, a conjecture is not a proven fact until someone can show a mathematical proof that works for every single number possible.

Even though computers have tested numbers up to incredibly large values (like 2⁶⁸, which is a huge number!), and they all eventually reach 1, no one has found a way to prove it for all numbers. This is why the Collatz conjecture is still one of the biggest unsolved puzzles in mathematics!

Images for kids

• 

  Histogram of total stopping times for the numbers 1 to 108. Total stopping time is on the x axis, frequency on the y axis.

• 

  Histogram of total stopping times for the numbers 1 to 109. Total stopping time is on the x axis, frequency on the y axis.

• 

  Iteration time for inputs of 2 to 107.

• 

  Total stopping time of numbers up to 250, 1000, 4000, 20000, 100000, 500000

• 

  Cobweb plot of the orbit 10-5-8-4-2-1-2-1-2-1-etc. in the real extension of the Collatz map (optimized by replacing "3n + 1" with "(3n + 1)/2")

• 

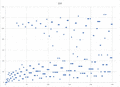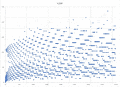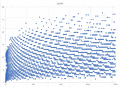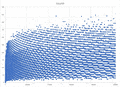
  Collatz map fractal in a neighbourhood of the real line

• 

  The x axis represents starting number, the y axis represents the highest number reached during the chain to 1. This plot shows a restricted y axis: some x values produce intermediates as high as 2.7×10⁷ (for x = 9663)

• 

  The number of iterations it takes to get to one for the first 100 million numbers.

See also

In Spanish: Conjetura de Collatz para niños