Mandelbrot set Facts for Kids

The Mandelbrot set

The Mandelbrot set is a famous and beautiful shape found in mathematics. It's a special kind of fractal, which means it has patterns that repeat themselves at different sizes. Imagine zooming in on a part of the shape, and you'd see smaller versions of the whole shape appearing again and again!

This amazing set is named after Benoît Mandelbrot, a mathematician who helped us understand these complex shapes. The Mandelbrot set is also important in a field called chaos theory, which studies how small changes can lead to very different outcomes.

The edges of the Mandelbrot set show something called self-similarity. This means that if you zoom in on its border, you'll find tiny copies of the entire set, even though they might be a bit squished or changed.

How the Mandelbrot Set is Made
Discovering the Mandelbrot Set
Creating Images of the Set
Variations of the Mandelbrot Set
- Multibrot Sets
Images for kids
See also

How the Mandelbrot Set is Made

The Mandelbrot set is created using a simple equation: z_n+1 = z_n² + c.

Understanding the Equation

In this equation, c and z are special kinds of numbers called complex numbers. These numbers have two parts: a regular number part and an "imaginary" part (like the square root of -1).
The letter n is a positive integer (a whole number like 0, 1, 2, 3, and so on).
We always start with z₀ = 0.

Finding Points in the Set

To find out if a number c belongs to the Mandelbrot set, we put it into the equation and repeat the calculation many times. This is called an iterative process.

If the value of z_n never gets super big (it stays within a certain limit), then c is part of the Mandelbrot set.
If z_n keeps growing larger and larger, heading towards infinity, then c is not part of the set.

An Example: Not in the Set

Let's try an example where c = 1:

Start with z₀ = 0.
z₁ = 0² + 1 = 1
z₂ = 1² + 1 = 2
z₃ = 2² + 1 = 5
z₄ = 5² + 1 = 26

As you can see, the numbers are getting bigger very quickly. They will keep growing towards infinity. So, because of this, the number 1 is not part of the Mandelbrot set.

An Example: In the Set

Now, let's try an example where c is equal to i (the square root of -1):

Start with z₀ = 0.
z₁ = 0² + i = i
z₂ = i² + i = -1 + i
z₃ = (-1 + i)² + i = (1 - 2i + i²) + i = (1 - 2i - 1) + i = -2i + i = -i
z₄ = (-i)² + i = -1 + i
z₅ = (-1 + i)² + i = -i

In this case, the numbers repeat: 0, i, (-1 + i), -i, (-1 + i), -i... They don't go off to infinity. This means that i is part of the Mandelbrot set.

Discovering the Mandelbrot Set

Benoît Mandelbrot was one of the first people to use computer graphics to create and show fractal images. He discovered the Mandelbrot set in 1979. He had access to powerful IBM computers, which helped him visualize these complex shapes.

Mandelbrot showed how very simple rules could create incredibly detailed and complex pictures. He explained that things we often think of as "rough" or "chaotic," like clouds or shorelines, actually have a hidden "degree of order" within them. Even though the equation z_n+1 = z_n² + c was known for a long time, Mandelbrot was the first to use computers to see what it looked like.

Creating Images of the Set

To make an image of the Mandelbrot set, computers apply the equation to every tiny dot (called a pixel) on the screen. Each pixel's position on the screen is used to get the number 'c'. The computer then checks if that 'c' value belongs to the set.

If 'c' is in the Mandelbrot set, the pixel is usually colored black (as seen in the main image on this page).
If 'c' is not in the set, the pixel is colored based on how quickly its numbers grew towards infinity. This is what creates the beautiful, colorful patterns around the black shape.

When the entire set is graphed, the resulting image is truly amazing, colorful, and easy to recognize.

Variations of the Mandelbrot Set

There are many different versions of the Mandelbrot set. Some popular ones include Multibrot, Buddhabrot, and Nebulabrot.

Multibrot Sets

Multibrot sets are a more general version of the Mandelbrot set. Instead of always using a power of 2 (like z²), they allow any exponent. The equation for a Multibrot set is: z_n+1 = z_n^d + c.

Here, d can be any number.
When d = 2, the Multibrot set is exactly the same as the original Mandelbrot set.

Images for kids

The Mandelbrot set (black) within a continuously colored environment
Mandelbrot animation based on a static number of iterations per pixel
Mandelbrot set detail
Zooming into the boundary of the Mandelbrot set
The first published picture of the Mandelbrot set, by Robert W. Brooks and Peter Matelski in 1978
Correspondence between the Mandelbrot set and the bifurcation diagram of the logistic map
With z_{n} iterates plotted on the vertical axis, the Mandelbrot set can be seen to bifurcate where the set is finite
External rays of wakes near the period 1 continent in the Mandelbrot set
Periods of hyperbolic components
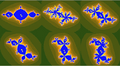
Attracting cycles and Julia sets for parameters in the 1/2, 3/7, 2/5, 1/3, 1/4, and 1/5 bulbs
Self-similarity in the Mandelbrot set shown by zooming in on a round feature while panning in the negative-x direction. The display center pans left from the fifth to the seventh round feature (-1.4002, 0) to (-1.4011, 0) while the view magnifies by a factor of 21.78 to approximate the square of the Feigenbaum ratio \delta.
A 4D Julia set may be projected or cross-sectioned into 3D, and because of this a 4D Mandelbrot is also possible.
$Mandelbar fractal from XaoS$

Image of the Tricorn / Mandelbar fractal
Start. Mandelbrot set with continuously colored environment.
Gap between the "head" and the "body", also called the "seahorse valley"
Double-spirals on the left, "seahorses" on the right
"Seahorse" upside down
Animated gradient structure inside the Mandelbrot set
Animated gradient structure inside the Mandelbrot set, detail
Rendering of progressive iterations from 285 to approximately 200,000 with corresponding bounded gradients animated
Thumbnail for gradient in progressive iterations