Chaos theory facts for kids
Chaos theory is a part of mathematics. It studies certain systems that are very sensitive. This means a tiny change at the beginning can make the system act totally differently later on.
Imagine trying to predict the weather. Even huge computers can't tell us what the weather will be like more than a few days from now. Why? Because the weather is a chaotic system. A very small change, like a tiny gust of wind from a butterfly's wings, can eventually lead to a completely different weather pattern. This idea is sometimes called the "butterfly effect."
At first glance, some systems, like the weather, might seem completely random. But chaos theory suggests that these patterns might not be random at all. If we look closely enough, we might find hidden patterns within them. The main idea is that a small difference at the start of something can lead to a huge change as time goes on.
Contents
What is Chaos Theory?
Chaos theory helps us understand complex systems. These are systems where many things are happening at once. Even a tiny change in one part can have a big effect on the whole system.
Sensitive Dependence on Initial Conditions
This is a key idea in chaos theory. It means that if you start a chaotic system in a slightly different way, it will end up looking very different later on. Think of it like rolling a ball down a hill. If you move your hand just a tiny bit when you let go, the ball might end up in a completely different spot at the bottom.
The Butterfly Effect
The "butterfly effect" is a famous example of sensitive dependence. It suggests that a butterfly flapping its wings in one part of the world could eventually cause a hurricane in another part. While this is a simplified example, it shows how small actions can have big, unexpected results in chaotic systems.
Examples of Chaotic Systems
Many things around us show chaotic behavior. Understanding these examples helps us see chaos theory in action.
Double Pendulums
Imagine a simple pendulum swinging back and forth. Now, attach a second pendulum to the end of the first one. This is called a double pendulum. If you try to start it in the exact same position twice, it's almost impossible. Even a tiny, invisible difference in how you start it will make the two swings look completely different very quickly.
Fractals and Chaos
A very important part of chaos theory is the study of special mathematical functions called fractals. Fractals are shapes that look the same no matter how much you zoom in or out. They are often linked to chaotic systems because a small change in their starting numbers can create very different and complex patterns. Because fractals are mathematical, they are easier to study than real-world chaotic systems.
Related Ideas
Images for kids
-
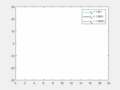
Lorenz equations used to generate plots for the y variable. The initial conditions for x and z were kept the same but those for y were changed between 1.001, 1.0001 and 1.00001. The values for \rho, \sigma and \beta were 45.92, 16 and 4 respectively. As can be seen from the graph, even the slightest difference in initial values causes significant changes after about 12 seconds of evolution in the three cases. This is an example of sensitive dependence on initial conditions.
-
Six iterations of a set of states [x,y] passed through the logistic map. The first iterate (blue) is the initial condition, which essentially forms a circle. Animation shows the first to the sixth iteration of the circular initial conditions. It can be seen that mixing occurs as we progress in iterations. The sixth iteration shows that the points are almost completely scattered in the phase space. Had we progressed further in iterations, the mixing would have been homogeneous and irreversible. The logistic map has equation x_{k+1} = 4 x_k (1 - x_k ). To expand the state-space of the logistic map into two dimensions, a second state, y, was created as y_{k+1} = x_k + y_k , if x_k + y_k
-
The map defined by x → 4 x (1 – x) and y → (x + y) mod 1 also displays topological mixing. Here, the blue region is transformed by the dynamics first to the purple region, then to the pink and red regions, and eventually to a cloud of vertical lines scattered across the space.
-
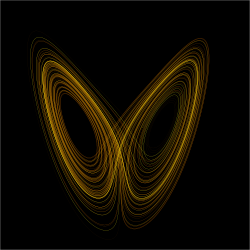
The Lorenz attractor displays chaotic behavior. These two plots demonstrate sensitive dependence on initial conditions within the region of phase space occupied by the attractor.
-
Turbulence in the tip vortex from an airplane wing. Studies of the critical point beyond which a system creates turbulence were important for chaos theory, analyzed for example by the Soviet physicist Lev Landau, who developed the Landau-Hopf theory of turbulence. David Ruelle and Floris Takens later predicted, against Landau, that fluid turbulence could develop through a strange attractor, a main concept of chaos theory.
-
A conus textile shell, similar in appearance to Rule 30, a cellular automaton with chaotic behaviour.
-
The red cars and blue cars take turns to move; the red ones only move upwards, and the blue ones move rightwards. Every time, all the cars of the same colour try to move one step if there is no car in front of it. Here, the model has self-organized in a somewhat geometric pattern where there are some traffic jams and some areas where cars can move at top speed.
See also
 In Spanish: Teoría del caos para niños
In Spanish: Teoría del caos para niños