Continuous function Facts for Kids

A mathematical function is called continuous if, simply put, a very small change in what you put into it (the input) only causes a very small change in what comes out (the output). If this doesn't happen, the function is discontinuous.

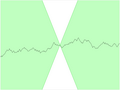
For functions that use real numbers as input and output, you can imagine their graph as an unbroken line or curve. You can draw this line without ever lifting your pen from the page. This idea of continuity was first described by Augustin-Louis Cauchy.

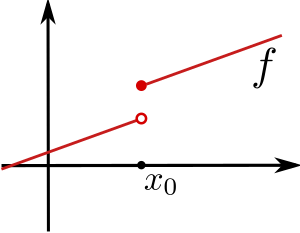
Imagine a function named f. At a specific point, let's call it 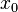$x_0$ , the function has a certain value, 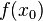$f(x_0)$ . If the function is continuous at 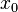$x_0$ , it means that if you pick any point x that is very, very close to 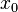$x_0$ , then the value of the function at x (which is 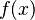$f(x)$ ) will be very, very close to 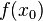$f(x_0)$ . The closer x gets to 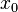$x_0$ , the closer 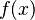$f(x)$ gets to $f(x_0)$ .

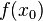There are also special types of continuous functions, like Lipschitz-continuous functions. These functions have a limit on how quickly their values can change. It means there's a maximum "steepness" or slope they can have anywhere on their graph.

This picture shows one type of discontinuous function. See how the line "jumps"?

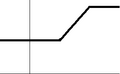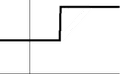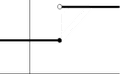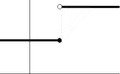
A simple way to check if a function is continuous is to use a pencil or your finger. Start at the left side of the function's graph. Then, move your finger or pencil along the path of the function. If you ever have to lift your finger or pencil to keep following the function's line, then you know it is not continuous. This is because when you lift your finger, you "jump" from one part of the function to another. This means a tiny movement of your finger caused a very big change in the function's value. This is exactly what the first sentence of this article means.

Chaos theory

Images for kids

A sequence of continuous functions f_n(x) whose (pointwise) limit function f(x) is discontinuous. The convergence is not uniform.
For a Lipschitz continuous function, there is a double cone (shown in white) whose vertex can be translated along the graph, so that the graph always remains entirely outside the cone.

Continuous function facts for kids

Related pages

Images for kids

See also