Complex number facts for kids

A complex number is a special kind of number that helps us solve math problems that regular numbers can't. Imagine a number that's made up of two parts: a "real" part and an "imaginary" part.

The most important imaginary number is called i. What makes i special is that when you multiply it by itself (square it), you get -1. That's pretty cool, because no regular number can do that! For example, 2 squared is 4, and -2 squared is also 4. So, i is a totally new kind of number.

All other imaginary numbers are just i multiplied by a regular number. Think of it like how all regular numbers can be seen as 1 multiplied by another number.

Mathematicians invented complex numbers to solve equations that had no answers using only real numbers. For example, if you have an equation like x² = -1, there's no real number you can put in for x that will make it true. But with i, the answer is simple: x = i!

The first mathematicians to think about these numbers were Gerolamo Cardano and Raffaele Bombelli in the 1500s. Later, Leonhard Euler started using the letter i to represent this special imaginary number.

Every complex number can be written in the form a + bi. Here, 'a' is the real part, and 'b' is the imaginary part. Both 'a' and 'b' are regular (real) numbers. For example, 3 + 2i is a complex number, where 3 is the real part and 2 is the imaginary part. Even regular numbers can be seen as complex numbers, like 5, which can be written as 5 + 0i.

The group of all complex numbers is often written as .

Doing Math with Complex Numbers

You can do all the usual math operations with complex numbers, just like with regular numbers! This includes addition, subtraction, multiplication, and division (as long as you don't divide by zero). They also follow the same rules as real numbers, like the commutative property (order doesn't matter for addition/multiplication) and the distributive property.

Adding and Subtracting

Adding complex numbers is easy! You just add the real parts together and the imaginary parts together.

• If you have (a + bi) and (c + di), their sum is (a + c) + (b + d)i.
• For example, (3 + 2i) + (1 + 4i) = (3+1) + (2+4)i = 4 + 6i.

Subtracting works the same way: subtract the real parts and the imaginary parts.

• (3 + 2i) - (1 + 4i) = (3-1) + (2-4)i = 2 - 2i.

Multiplying Complex Numbers

Multiplying complex numbers is a bit different because of i² = -1.

• If you multiply (a + bi) by (c + di), you get:

* (ac - bd) + (bc + ad)i.

• Let's try an example: (1 + 2i) multiplied by (3 + 4i).

* (1 × 3) + (1 × 4i) + (2i × 3) + (2i × 4i) * 3 + 4i + 6i + 8i² * Since i² is -1, this becomes: 3 + 4i + 6i - 8 * Combine the real parts and imaginary parts: (3 - 8) + (4 + 6)i = -5 + 10i.

Complex Conjugation

There's a special operation called conjugation. The complex conjugate of a number like (a + bi) is (a - bi). You just change the sign of the imaginary part.

• For example, the conjugate of (3 + 2i) is (3 - 2i).

This is useful because when you multiply a complex number by its conjugate, the result is always a real number!

• (a + bi) × (a - bi) = a² - (bi)² = a² - b²i² = a² - b²(-1) = a² + b².
• For example, (3 + 2i) × (3 - 2i) = 3² + 2² = 9 + 4 = 13.

Showing Complex Numbers Visually

A complex number can be shown as a point or a vector on a special graph called the Argand diagram.

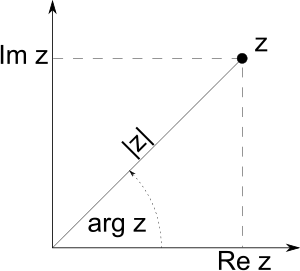
You can draw complex numbers on a special graph called the complex plane. It looks a lot like a regular graph with an x-axis and a y-axis.

• The horizontal line is the "real axis" (like the x-axis).
• The vertical line is the "imaginary axis" (like the y-axis).

If you have a complex number like z = a + bi, you can find it on this plane by going 'a' units along the real axis and 'b' units up or down the imaginary axis. This point can also be seen as an arrow (or vector) starting from the center (0,0) and ending at the point (a,b).

Modulus and Argument

When you draw this arrow, you can measure two things:

• The modulus (written as 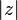) is the length of the arrow from the center to the point. You can find this using the Pythagorean theorem: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sqrt{a^2 + b^2} .
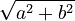• The argument (written as 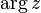) is the angle the arrow makes with the positive real axis, measured counterclockwise.

These two measurements (length and angle) give you another way to describe a complex number, which is useful in higher math!

Why Complex Numbers are Important

Complex numbers are super important in many areas of math and science. One big reason is the Fundamental theorem of algebra. This theorem basically says that with complex numbers, every polynomial equation (like x² + 2x + 1 = 0) has a solution. Before complex numbers, many equations had no answers!

The invention of complex numbers also opened the door to even more types of numbers, like hypercomplex numbers and quaternions, which help solve even more complex problems in fields like physics and engineering. They show us that numbers can be much more varied and interesting than we might first think!

Images for kids

• 

  The Mandelbrot set, a famous fractal pattern created using complex numbers.

See also

In Spanish: Número complejo para niños