Fundamental theorem of algebra facts for kids
The fundamental theorem of algebra is a very important rule in mathematics. It helps us understand polynomials. A polynomial is a special kind of math expression, like 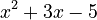 . This theorem tells us how many answers, or "roots," a polynomial equation can have. It was first proven by the famous German mathematician Carl Friedrich Gauss.
. This theorem tells us how many answers, or "roots," a polynomial equation can have. It was first proven by the famous German mathematician Carl Friedrich Gauss.
This theorem says that for any polynomial equation like 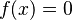 , if the highest power of
, if the highest power of  in it is
in it is  (and
(and  is greater than zero), then there must be at least one answer for
is greater than zero), then there must be at least one answer for  . In fact, if you count all types of answers, there will be exactly
. In fact, if you count all types of answers, there will be exactly  answers!
answers!
Contents
What is a Polynomial?
A polynomial is a math expression made of variables (like  ) and numbers, combined using addition, subtraction, and multiplication. The variable can only have whole number powers (like
) and numbers, combined using addition, subtraction, and multiplication. The variable can only have whole number powers (like 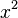 ,
, 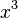 , but not
, but not 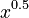 ).
).
For example, 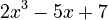 is a polynomial.
is a polynomial.
- The numbers
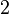 ,
, 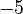 , and
, and 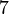 are called coefficients.
are called coefficients. - The variable is
 .
. - The powers of
 are
are 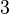 ,
, 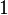 (for
(for  ), and
), and 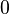 (for the number
(for the number 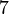 , which is like
, which is like 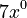 ).
).
Understanding the Degree of a Polynomial
The degree of a polynomial is the highest power of the variable in the expression.
- In
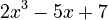 , the highest power of
, the highest power of  is
is 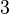 . So, its degree is
. So, its degree is 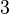 .
. - For
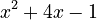 , the highest power is
, the highest power is 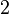 . Its degree is
. Its degree is 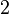 .
. - For
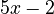 , the highest power is
, the highest power is 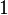 . Its degree is
. Its degree is 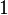 .
.
The fundamental theorem of algebra connects the degree of a polynomial to the number of its roots.
What are Polynomial Roots?
A root of a polynomial equation is a value for the variable that makes the whole equation equal to zero. Imagine you have the polynomial 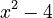 . If you set it equal to zero:
. If you set it equal to zero: 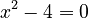 . The roots are the values of
. The roots are the values of  that make this true.
that make this true.
- If
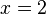 , then
, then  . So,
. So, 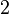 is a root.
is a root. - If
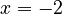 , then
, then 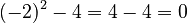 . So,
. So, 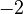 is also a root.
is also a root.
For 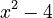 , the degree is
, the degree is 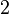 , and it has exactly
, and it has exactly 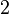 roots (
roots (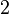 and
and 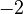 ). This matches what the theorem says!
). This matches what the theorem says!
Counting All the Roots
The theorem says a polynomial of degree  has exactly
has exactly  roots. This is true if we consider two special cases:
roots. This is true if we consider two special cases:
Complex Numbers as Roots
Sometimes, the roots are not just regular numbers (like 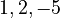 ). They can be complex numbers. Complex numbers involve the imaginary unit
). They can be complex numbers. Complex numbers involve the imaginary unit 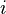 , where
, where 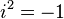 . For example, the polynomial
. For example, the polynomial 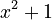 has a degree of
has a degree of 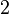 . If you set
. If you set 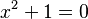 , then
, then 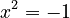 . The roots are
. The roots are 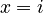 and
and 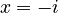 . These are complex numbers.
. These are complex numbers.
Repeated Roots
Sometimes, a root can appear more than once. This is called a "repeated root" or "multiple root." Consider the polynomial 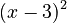 , which is
, which is 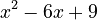 . Its degree is
. Its degree is 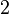 . If you set
. If you set 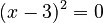 , the only value that works is
, the only value that works is 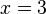 . But the theorem says there should be two roots. In this case, we count
. But the theorem says there should be two roots. In this case, we count 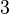 twice. So, the roots are
twice. So, the roots are 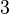 and
and 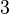 . This way, the count of roots always matches the degree.
. This way, the count of roots always matches the degree.
Why is this Theorem Important?
The fundamental theorem of algebra is a cornerstone of mathematics. It tells us that every polynomial equation has a complete set of solutions. This is very useful in many areas of science and engineering, like designing circuits, understanding physics, or even creating computer graphics. It guarantees that we can always find all the answers to these types of equations.
See also
 In Spanish: Teorema fundamental del álgebra para niños
In Spanish: Teorema fundamental del álgebra para niños

