
This picture shows 3 groups of 5, which equals 15.
Multiplication is a basic math operation. It helps you find the product of two numbers. Think of it as a quick way to do repeated addition.
For example, if you have 3 groups of 5 apples, multiplication helps you find the total number of apples quickly. You would write this as 3 × 5 = 15. You can also say "three times five equals fifteen."
When you multiply natural numbers (like 1, 2, 3...), it's like figuring out how many small squares fit into a rectangle. One number tells you how many squares are on one side, and the other number tells you how many squares are on the other side.
For real numbers (which include fractions and decimals), multiplication can tell you the area of a rectangle. One number is the length of one side, and the other number is the length of the other side.
What are the parts of a multiplication problem?
In a multiplication problem like 3 × 5 = 15:
- The numbers you multiply (like 3 and 5) are called factors.
- The answer you get (like 15) is called the product.
Does the order of numbers matter?
For most numbers you use every day, the order in which you multiply them does not change the answer. This is called the commutative property. For example, 4 × 6 gives you the same answer as 6 × 4. Both equal 24. This is true for:
However, for some more advanced math concepts like quaternions or matrices, the order can matter! But you won't usually see those until higher levels of math.
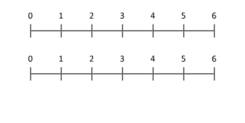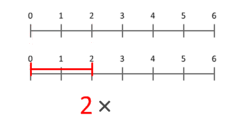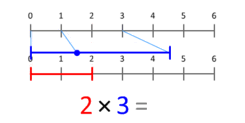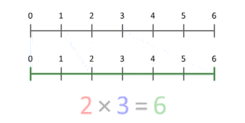
This animation shows how multiplying by 2 scales the length of 3 to become 6.
Multiplication as scaling
You can also think of multiplication as scaling a quantity. Imagine you have a length of 3 units. If you multiply it by 2, you are scaling that length to be twice as long, making it 6 units. The animation shows this idea. The blue dot starts at 1 and moves to the end of the red segment, showing the scaling.
Multiplication and division
The opposite of multiplication is division. If you know that 3 × 5 = 15, then you also know that 15 ÷ 3 = 5 and 15 ÷ 5 = 3.
Multiplication table
Many teachers ask students to memorize the multiplication table for the first 9 or 12 numbers. This helps you quickly solve multiplication problems without needing a calculator.
Multiplication table
Table of 1
| 1 |
× |
0 |
= |
0 |
| 1 |
× |
1 |
= |
1 |
| 1 |
× |
2 |
= |
2 |
| 1 |
× |
3 |
= |
3 |
| 1 |
× |
4 |
= |
4 |
| 1 |
× |
5 |
= |
5 |
| 1 |
× |
6 |
= |
6 |
| 1 |
× |
7 |
= |
7 |
| 1 |
× |
8 |
= |
8 |
| 1 |
× |
9 |
= |
9 |
| 1 |
× |
10 |
= |
10 |
|
Table of 2
| 2 |
× |
0 |
= |
0 |
| 2 |
× |
1 |
= |
2 |
| 2 |
× |
2 |
= |
4 |
| 2 |
× |
3 |
= |
6 |
| 2 |
× |
4 |
= |
8 |
| 2 |
× |
5 |
= |
10 |
| 2 |
× |
6 |
= |
12 |
| 2 |
× |
7 |
= |
14 |
| 2 |
× |
8 |
= |
16 |
| 2 |
× |
9 |
= |
18 |
| 2 |
× |
10 |
= |
20 |
|
Table of 3
| 3 |
× |
0 |
= |
0 |
| 3 |
× |
1 |
= |
3 |
| 3 |
× |
2 |
= |
6 |
| 3 |
× |
3 |
= |
9 |
| 3 |
× |
4 |
= |
12 |
| 3 |
× |
5 |
= |
15 |
| 3 |
× |
6 |
= |
18 |
| 3 |
× |
7 |
= |
21 |
| 3 |
× |
8 |
= |
24 |
| 3 |
× |
9 |
= |
27 |
| 3 |
× |
10 |
= |
30 |
|
Table of 4
| 4 |
× |
0 |
= |
0 |
| 4 |
× |
1 |
= |
4 |
| 4 |
× |
2 |
= |
8 |
| 4 |
× |
3 |
= |
12 |
| 4 |
× |
4 |
= |
16 |
| 4 |
× |
5 |
= |
20 |
| 4 |
× |
6 |
= |
24 |
| 4 |
× |
7 |
= |
28 |
| 4 |
× |
8 |
= |
32 |
| 4 |
× |
9 |
= |
36 |
| 4 |
× |
10 |
= |
40 |
|
Table of 5
| 5 |
× |
0 |
= |
0 |
| 5 |
× |
1 |
= |
5 |
| 5 |
× |
2 |
= |
10 |
| 5 |
× |
3 |
= |
15 |
| 5 |
× |
4 |
= |
20 |
| 5 |
× |
5 |
= |
25 |
| 5 |
× |
6 |
= |
30 |
| 5 |
× |
7 |
= |
35 |
| 5 |
× |
8 |
= |
40 |
| 5 |
× |
9 |
= |
45 |
| 5 |
× |
10 |
= |
50 |
|
Table of 6
| 6 |
× |
0 |
= |
0 |
| 6 |
× |
1 |
= |
6 |
| 6 |
× |
2 |
= |
12 |
| 6 |
× |
3 |
= |
18 |
| 6 |
× |
4 |
= |
24 |
| 6 |
× |
5 |
= |
30 |
| 6 |
× |
6 |
= |
36 |
| 6 |
× |
7 |
= |
42 |
| 6 |
× |
8 |
= |
48 |
| 6 |
× |
9 |
= |
54 |
| 6 |
× |
10 |
= |
60 |
|
Table of 7
| 7 |
× |
0 |
= |
0 |
| 7 |
× |
1 |
= |
7 |
| 7 |
× |
2 |
= |
14 |
| 7 |
× |
3 |
= |
21 |
| 7 |
× |
4 |
= |
28 |
| 7 |
× |
5 |
= |
35 |
| 7 |
× |
6 |
= |
42 |
| 7 |
× |
7 |
= |
49 |
| 7 |
× |
8 |
= |
56 |
| 7 |
× |
9 |
= |
63 |
| 7 |
× |
10 |
= |
70 |
|
Table of 8
| 8 |
× |
0 |
= |
0 |
| 8 |
× |
1 |
= |
8 |
| 8 |
× |
2 |
= |
16 |
| 8 |
× |
3 |
= |
24 |
| 8 |
× |
4 |
= |
32 |
| 8 |
× |
5 |
= |
40 |
| 8 |
× |
6 |
= |
48 |
| 8 |
× |
7 |
= |
56 |
| 8 |
× |
8 |
= |
64 |
| 8 |
× |
9 |
= |
72 |
| 8 |
× |
10 |
= |
80 |
|
Table of 9
| 9 |
× |
0 |
= |
0 |
| 9 |
× |
1 |
= |
9 |
| 9 |
× |
2 |
= |
18 |
| 9 |
× |
3 |
= |
27 |
| 9 |
× |
4 |
= |
36 |
| 9 |
× |
5 |
= |
45 |
| 9 |
× |
6 |
= |
54 |
| 9 |
× |
7 |
= |
63 |
| 9 |
× |
8 |
= |
72 |
| 9 |
× |
9 |
= |
81 |
| 9 |
× |
10 |
= |
90 |
|
Table of 10
| 10 |
× |
0 |
= |
0 |
| 10 |
× |
1 |
= |
10 |
| 10 |
× |
2 |
= |
20 |
| 10 |
× |
3 |
= |
30 |
| 10 |
× |
4 |
= |
40 |
| 10 |
× |
5 |
= |
50 |
| 10 |
× |
6 |
= |
60 |
| 10 |
× |
7 |
= |
70 |
| 10 |
× |
8 |
= |
80 |
| 10 |
× |
9 |
= |
90 |
| 10 |
× |
10 |
= |
100 |
|
Other pages
Images for kids
-
This shows 4 × 5 = 20. The large rectangle is made up of 20 small squares.
-
Product of 45 and 256. This is a special way to multiply called Lattice multiplication. The final answer is 11,520.
See also
 In Spanish: Multiplicación para niños
In Spanish: Multiplicación para niños
 In Spanish: Multiplicación para niños
In Spanish: Multiplicación para niños







