Rectangle Facts for Kids

Quick facts for kids Rectangle
Rectangle
Type	quadrilateral, trapezium, parallelogram, orthotope
Edges and vertices	4
Schläfli symbol	{ } × { }
Coxeter diagram
Symmetry group	Dihedral (D₂), [2], (*22), order 4
Dual polygon	rhombus
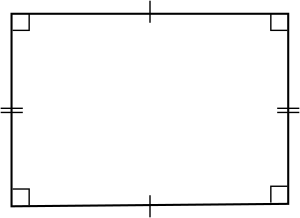
Properties	convex, isogonal, cyclic Opposite angles and sides are congruent

A rectangle is a flat shape with four straight sides. It also has four right angles. Think of a door or a book cover!

If a rectangle has all four sides the same length, it's called a square. Sometimes, a rectangle that is not a square is called an oblong.

The word "rectangle" comes from Latin. Rectus means "right" or "proper". Angulus means "angle". So, a rectangle literally means "right angle".

Rectangles are used in many tiling puzzles. You can use them to cover a flat surface without any gaps.

What Makes a Rectangle Special?
- Rectangle's Family Tree
Cool Facts About Rectangles
- Rectangle and Rhombus: A Duality
How to Measure a Rectangle
Interesting Rectangle Rules
Crossed Rectangles
Tiling with Rectangles
Images for kids
See also

What Makes a Rectangle Special?

A rectangle is a special type of parallelogram and trapezoid. A square is a special type of rectangle.

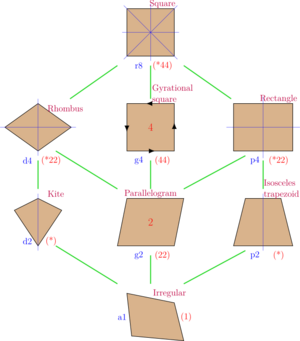
A rectangle is a special kind of shape called a quadrilateral. A quadrilateral is any shape with four sides.

Rectangle's Family Tree

A rectangle is a special type of parallelogram. In a parallelogram, opposite sides are parallel and equal in length. What makes a rectangle different is that all its angles are right angles (90 degrees).

A parallelogram is also a special type of trapezoid. A trapezoid is a shape with at least one pair of parallel sides.

So, a rectangle is part of a bigger family of shapes!

Cool Facts About Rectangles

Rectangles have some interesting features:

They are cyclic. This means all four corners of a rectangle can touch a single circle.
They are equiangular. This means all their corner angles are equal. Each angle is exactly 90 degrees.
They have two lines of reflectional symmetry. You can fold a rectangle in half in two ways, and both halves will match perfectly.
They also have rotational symmetry of order 2. This means you can turn a rectangle 180 degrees, and it will look exactly the same.

Rectangle and Rhombus: A Duality

A rhombus is a shape with four equal sides. It's like a diamond. Rectangles and rhombuses are opposites in some ways. This is called a "duality".

Rectangle	Rhombus
All angles are equal.	All sides are equal.
Opposite sides are equal.	Opposite angles are equal.
Its center is the same distance from its corners. It has a circumcircle.	Its center is the same distance from its sides. It has an incircle.
Two lines of symmetry cut through opposite sides.	Two lines of symmetry cut through opposite angles.
Diagonals are equal in length.	Diagonals cross at equal angles.

If you connect the middle points of a rectangle's sides, you get a rhombus! And if you do the same for a rhombus, you get a rectangle.

How to Measure a Rectangle

The formula for the perimeter of a rectangle

The area of a rectangle is the product of the length and width.

Let's say a rectangle has a length (how long it is) of 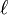$\ell$ and a width (how wide it is) of $w$ .

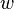The area ( $A$ ) is the space it covers. You find it by multiplying length by width:

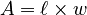
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A = \ell \times w

The perimeter ( 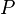$P$ ) is the distance around its outside edge. You find it by adding up all the sides:

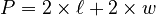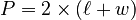
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P = 2 \times \ell + 2 \times w or Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): P = 2 \times (\ell + w)

The diagonal ( 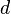$d$ ) is the line from one corner to the opposite corner. You can find its length using a special math rule called the Pythagorean theorem:

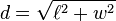
$d=\sqrt{\ell^2 + w^2}$

If the length and width are the same (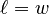Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \ell = w ), then the rectangle is a square!

Interesting Rectangle Rules

The isoperimetric theorem for rectangles says that for all rectangles with the same perimeter, the square will always have the biggest area.
If a parallelogram has diagonals that are equal in length, then it must be a rectangle.

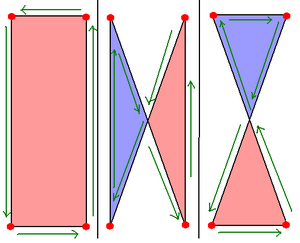
Crossed Rectangles

Crossed rectangles look like bow ties.

Imagine a rectangle, but then you cross its opposite sides. This creates a crossed rectangle. It looks a bit like a bow tie or a butterfly. Even though it crosses itself, it still has some things in common with a regular rectangle:

Opposite sides are equal in length.
The two diagonals are equal in length.
It has two lines of reflectional symmetry and rotational symmetry of order 2 (180 degrees).

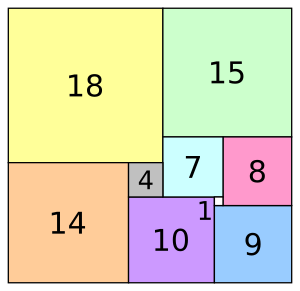
Tiling with Rectangles

A perfect rectangle made of 9 smaller squares.

Sometimes, a large rectangle can be completely covered, or "tiled," by smaller shapes.

If a rectangle is tiled by squares, it's called a "squared" rectangle.
If it's tiled by other rectangles, it's a "rectangled" rectangle.
If it's tiled by triangles, it's a "triangulated" rectangle.

A tiling is called perfect if all the smaller shapes are different sizes. If some are the same size, it's imperfect. You can find many examples of these tilings online at squaring.net.

The smallest number of squares needed to perfectly tile a rectangle is 9. For a square, it's 21. These were found using computers in 1978!

Images for kids

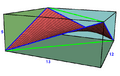
A saddle rectangle has 4 non-flat corners. It forms a unique minimal surface inside a cuboid.

Rectangle facts for kids

Contents