Rhombus facts for kids
Quick facts for kids Rhombus |
|
|---|---|
Two rhombi
|
|
| Type | quadrilateral, parallelogram, kite |
| Edges and vertices | 4 |
| Schläfli symbol | { } + { } |
| Coxeter diagram | |
| Symmetry group | Dihedral (D2), [2], (*22), order 4 |
| Dual polygon | rectangle |
| Properties | convex, isotoxal |
A rhombus is a special type of parallelogram where all four sides are exactly the same length. Think of it like a square that has been pushed over, so its angles are no longer 90 degrees. If a rhombus does have all its angles equal (which means they must all be 90 degrees), then it's called a square.
The word rhombus comes from the Greek word rhombos. This word meant "spinning top" or "something that spins". Sometimes people call a rhombus a "diamond shape," but not all rhombi look like the diamonds on playing cards.
To find the perimeter of a rhombus, you just add up the lengths of all its sides. Since all sides are equal, you can also just multiply the length of one side by four! Just like other parallelograms, a rhombus has opposite sides that are parallel, and its opposite angles are equal.
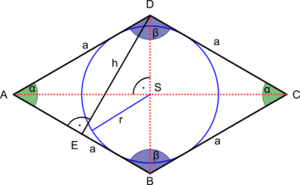
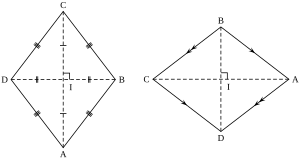
Another cool thing about a rhombus is its diagonals. These are the lines that connect opposite corners (like the dashed lines in the second picture). These diagonals always cross each other exactly in the middle, and they meet at a perfect right angle (90 degrees).
Contents
What Makes a Rhombus Special?
A shape with four sides (called a quadrilateral) is a rhombus if it has any of these features:
- It's a parallelogram where a diagonal cuts one of its inside angles exactly in half.
- It's a parallelogram where at least two sides next to each other are the same length.
- It's a parallelogram where the diagonals cross each other at a 90-degree angle.
- It's a quadrilateral where all four sides are the same length (this is the main definition!).
- It's a quadrilateral where the diagonals cross at a right angle and also cut each other in half.
- It's a quadrilateral where each diagonal cuts two opposite inside angles exactly in half.
Key Features of a Rhombus
Every rhombus has two diagonals that connect its opposite corners. It also has two pairs of parallel sides. Because of how it's shaped, a rhombus is symmetrical across each of its diagonals. This means if you fold a rhombus along a diagonal, the two halves will match perfectly.
Here are some important features of a rhombus:
- The angles that are opposite each other in a rhombus always have the same size.
- The two diagonals of a rhombus always cross each other at a right angle (90 degrees).
- The diagonals also cut the opposite angles in half.
Since opposite sides are parallel and opposite angles are equal, every rhombus is also a parallelogram. This means a rhombus shares all the properties of a parallelogram. For example, its adjacent angles (angles next to each other) add up to 180 degrees. Also, its two diagonals always cut each other in half.
Not every parallelogram is a rhombus. But any parallelogram where the diagonals cross at a right angle is a rhombus. A rhombus is also a type of kite. A kite is a shape with two pairs of equal-length sides that are next to each other. If a shape is both a kite and a parallelogram, then it must be a rhombus.
A rhombus is also a "tangential quadrilateral." This means you can draw a perfect circle inside it that touches all four of its sides.
How Long Are the Diagonals?
You can figure out the length of the diagonals (let's call them p and q) if you know the side length (a) and one of the angles (α) of the rhombus. These lengths are found using special math rules called the law of cosines.
How to Find the Area
Just like any parallelogram, you can find the area K of a rhombus by multiplying its base (any side length a) by its height (h). The height is the straight distance between two parallel sides:
- K = a × h
You can also find the area using the side length and one of its angles:
- K = a² × sin(angle)
Another common way to find the area is by using the lengths of its two diagonals, p and q:
- K = (p × q) / 2
Finally, you can find the area using the side length (a) and the radius (r) of the circle that can be drawn inside the rhombus:
- K = 2a × r
Rhombus vs. Rectangle
A rhombus and a rectangle are like opposites in some ways:
- A rhombus has all sides equal, but a rectangle has all angles equal (at 90 degrees).
- A rhombus has opposite angles equal, while a rectangle has opposite sides equal.
- You can draw a circle inside a rhombus that touches all its sides. For a rectangle, you can draw a circle around it that touches all its corners.
- A rhombus has lines of symmetry that go through its opposite corners. A rectangle has lines of symmetry that go through the middle of its opposite sides.
- The diagonals of a rhombus cross at equal angles (90 degrees). The diagonals of a rectangle are equal in length.
- If you connect the middle points of the sides of a rhombus, you get a rectangle. And if you connect the middle points of the sides of a rectangle, you get a rhombus!
Other Cool Facts
- The rhombus shape is used in one of the five basic ways to arrange points in a repeating pattern, called a "rhombic lattice."
- You can use identical rhombi to cover a flat surface (like a floor) in three different ways without any gaps or overlaps. One famous example is the "rhombille tiling," which uses rhombi with 60-degree angles.
Images for kids
See also
 In Spanish: Rombo para niños
In Spanish: Rombo para niños