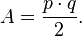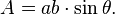Kite (geometry) facts for kids
Quick facts for kids Kite |
|
|---|---|
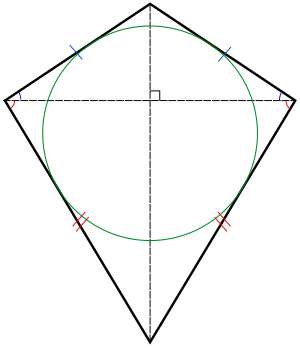
A kite, showing its pairs of equal length sides and its inscribed circle.
|
|
| Type | Quadrilateral |
| Edges and vertices | 4 |
| Symmetry group | D1 (*) |
| Dual polygon | Isosceles trapezoid |
In Euclidean geometry, a kite is a shape with four straight sides. It has two pairs of sides that are the same length. These equal sides are always next to each other. This is different from a parallelogram, which also has two pairs of equal sides, but those sides are opposite each other.
The geometric kite is named after the flying kites you see in the sky. These often have this shape. The flying toy is named after a type of bird. Sometimes, a geometric kite is also called a deltoid. However, this word can also mean a muscle in your shoulder or a different geometric curve.
A kite can be either convex (all angles point outwards) or concave (one angle points inwards). When a kite is concave, it is sometimes called a "dart" or "arrowhead."
Contents
Special Kites
Some shapes are special kinds of kites. For example, a rhombus (a shape with four equal sides) or a square (a shape with four equal sides and four right angles) can be thought of as kites. This is because their sides can be grouped into two pairs of equal, adjacent sides.
If a kite has all its sides the same length, it is a rhombus. If a kite has all its angles the same, it is a square.
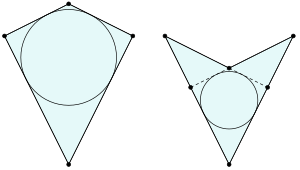
Some kites can fit perfectly inside a circle. These are called right kites. In these kites, the two angles on opposite sides of the kite's main line of symmetry are each 90 degrees (right angles). Right kites are special because they can also have a circle drawn inside them that touches all four sides.
Kites can be used to cover a flat surface without any gaps or overlaps. This is called tessellation or tiling. One type of right kite can tile a surface by reflecting itself over its edges. This creates a pattern called the deltoidal trihexagonal tiling.
 A right kite |
An equidiagonal kite |
What Makes a Kite a Kite?
A shape with four sides is a kite if any of these things are true:
- It has two pairs of equal sides that are next to each other (this is the main definition).
- One of its diagonals (a line connecting opposite corners) cuts the other diagonal exactly in half and at a 90-degree angle.
- One diagonal acts as a line of symmetry. This means it divides the kite into two identical triangles that are mirror images of each other.
- One diagonal cuts a pair of opposite angles exactly in half.
Symmetry of Kites
Kites are special because they have a line of symmetry along one of their diagonals. This means you could fold the kite along that diagonal, and both halves would match up perfectly.
Other shapes with a line of symmetry include isosceles trapezoids (where the line of symmetry passes through the middle of two sides). Shapes like the rhombus and rectangle have two lines of symmetry. A square is very symmetrical; it has four lines of symmetry.
Basic Features of Kites
Every kite has diagonals that cross each other at a right angle (90 degrees). This means kites are a type of orthodiagonal quadrilateral. Also, the diagonal that is the line of symmetry cuts the other diagonal exactly in half. It also cuts the two angles it passes through exactly in half.
One of the diagonals of a convex kite divides it into two isosceles triangles (triangles with two equal sides). The other diagonal (the line of symmetry) divides the kite into two congruent triangles (triangles that are exactly the same size and shape). The two inside angles of a kite that are on opposite sides of the symmetry line are always equal.
How to Find the Area
To find the area of a kite, you can use a simple formula. If p and q are the lengths of the two diagonals, the area A is:
This means you multiply the lengths of the diagonals together and then divide by 2.
Another way to find the area, if you know the lengths of the two different sides (let's call them a and b) and the angle θ between them, is:
Circles Inside and Outside Kites
Every convex kite can have a circle drawn inside it that touches all four of its sides. This is called an inscribed circle. Because of this, every convex kite is a tangential quadrilateral.
For every concave kite, there are also two circles that can touch all four sides (or their extended lines). One circle is inside the kite, touching the two sides that are not part of the inward-pointing angle. The other circle is outside the kite, touching the two sides that form the inward-pointing angle.
Kites and Trapezoids: Dual Shapes
Kites and isosceles trapezoids are considered "dual" shapes. This means they have opposite but related properties. For example, the "polar figure" of a kite is an isosceles trapezoid, and vice versa.
Here's how their properties compare:
| Isosceles trapezoid | Kite |
|---|---|
| Two pairs of equal angles next to each other | Two pairs of equal sides next to each other |
| One pair of equal opposite sides | One pair of equal opposite angles |
| A line of symmetry through one pair of opposite sides | A line of symmetry through one pair of opposite angles |
| Can have a circle drawn around it | Can have a circle drawn inside it |
Kites in Tiling and Polyhedra
All kites can tile a flat surface by flipping them over around the middle of their edges. This is true for all shapes with four sides.
Some 3D shapes, called polyhedra, have faces that are shaped like kites. Examples include the deltoidal icositetrahedron and the trapezohedron.
Kites and darts (concave kites) are also important in Penrose tiling. This is a special type of aperiodic tiling that covers a surface without repeating the pattern.
When a Tangential Quadrilateral is a Kite
A tangential quadrilateral (a shape with a circle inside it that touches all four sides) is a kite if any of these conditions are true:
- Its area is half the product of its diagonals.
- Its diagonals cross each other at a right angle. (So, kites are the only shapes that are both tangential and orthodiagonal.)
- The center of the circle inside the shape lies on a line of symmetry that is also a diagonal.
- Eric W. Weisstein, Kite at MathWorld.
See also
 In Spanish: Deltoide para niños
In Spanish: Deltoide para niños