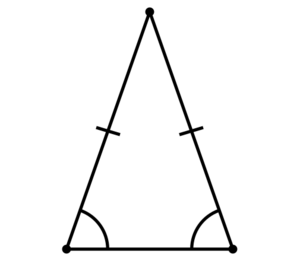
Isosceles triangle Facts for Kids

An isosceles triangle has two sides that are the same length.

In geometry, an isosceles triangle is a special kind of triangle. What makes it special is that it has two sides that are exactly the same length. These two equal sides are called the legs. The third side, which is usually different in length, is called the base.

Sometimes, an isosceles triangle is defined as having at least two equal sides. This means that an equilateral triangle, which has all three sides equal, can also be considered an isosceles triangle. Other examples include the isosceles right triangle (which has a 90-degree angle), the golden triangle, and shapes found in bipyramids.

People have studied isosceles triangles for a very long time, even in ancient Egyptian mathematics and Babylonian mathematics. They have also been used in art and building designs for thousands of years. You can often see them in the triangular parts of buildings, like the pediments and gables.

Every isosceles triangle has a special line running through its middle. This line is called an axis of symmetry. It perfectly divides the triangle into two mirror-image halves. The two angles opposite the equal sides are also always equal to each other. These angles are always acute (less than 90 degrees). The type of isosceles triangle (acute, right, or obtuse) depends only on the angle between its two equal legs.

Understanding Isosceles Triangles
- Key Parts of an Isosceles Triangle
- The Line of Symmetry
Calculating with Isosceles Triangles
Where You See Isosceles Triangles
- In Buildings and Design
- In Flags and Art
See also

Understanding Isosceles Triangles

Key Parts of an Isosceles Triangle

An isosceles triangle has specific parts that help us understand it:

Legs: These are the two sides that have the same length.
Base: This is the third side, which is usually a different length from the legs.
Apex: This is the corner where the two equal legs meet.
Base Angles: These are the two angles at the ends of the base. They are always equal to each other.
Apex Angle: This is the angle at the apex.

The Line of Symmetry

In any isosceles triangle, a special line goes from the apex straight down to the middle of the base. This line is very important because it does several things at once:

It is the altitude (the height) of the triangle. It forms a 90-degree angle with the base.
It is the angle bisector of the apex angle, meaning it cuts that angle exactly in half.
It is the median to the base, meaning it connects the apex to the midpoint of the base.
It is the perpendicular bisector of the base, meaning it cuts the base in half and is at a 90-degree angle to it.
It is the triangle's unique axis of symmetry.

This means that if you fold an isosceles triangle along this line, both halves will match up perfectly!

Calculating with Isosceles Triangles

We can use simple formulas to find the height, area, and perimeter of an isosceles triangle. Let's say the equal sides (legs) have a length of a, and the base has a length of b.

Finding the Height

The height (let's call it h) is the length of that special line from the apex down to the base. We can find it using the Pythagorean theorem. Imagine the height line splitting the isosceles triangle into two smaller, identical right triangles. Each of these right triangles has:

A hypotenuse (the longest side) equal to a (one of the legs of the isosceles triangle).
One leg equal to h (the height).
The other leg equal to b/2 (half of the base).

So, the formula for the height is: 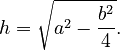$h=\sqrt{a^2-\frac{b^2}{4}}.$

Finding the Area

The area (let's call it T) of any triangle is half of its base multiplied by its height. Since we know the base (b) and we can find the height (h), the formula for the area of an isosceles triangle is: 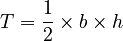Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): T=\frac{1}{2} \times b \times h Or, if you only know the leg length a and base b: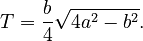 $T=\frac{b}{4}\sqrt{4a^2-b^2}.$

If you know the length of the legs (a) and the angle between them (the apex angle, let's call it 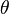$\theta$ ), you can also find the area using this formula: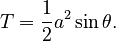 $T=\frac{1}{2}a^2\sin\theta.$

Finding the Perimeter

The perimeter (let's call it p) is the total distance around the outside of the triangle. Since an isosceles triangle has two equal sides (a) and one base (b), its perimeter is simply: 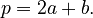$p = 2a + b.$

Where You See Isosceles Triangles

In Buildings and Design

Isosceles triangles are very common in architecture and design.

Gables and Pediments: These are the triangular parts at the top of buildings, often found in ancient Greek architecture and later styles. In ancient Greek buildings, these triangles were often wide and flat (obtuse isosceles). In Gothic architecture, they became taller and sharper (acute isosceles).
Warren Trusses: These are structures used in bridges and roofs. They are often made up of many isosceles triangles connected together to provide strength.

Obtuse isosceles pediment of the Pantheon, Rome

Acute isosceles gable over the Saint-Etienne portal, Notre-Dame de Paris

Detailed view of a modified Warren truss with verticals

In Flags and Art

Isosceles triangles are also popular in graphic design and decorative arts.

Flags: Many flags around the world use isosceles triangles as part of their design. For example, the flag of Guyana has a large green isosceles triangle pointing to the right. The flag of Saint Lucia uses two isosceles triangles to represent its twin mountains.
Religious Symbols: They can also be found in symbols with special meanings, like the Sri Yantra in Hindu practices.

The Flag of Guyana uses an isosceles triangle.

The Flag of Saint Lucia features two isosceles triangles.

Isosceles triangle facts for kids

Contents