Euclidean geometry facts for kids
Euclidean geometry is a special way of understanding geometry in mathematics. It's named after an ancient Greek mathematician called Euclid. He wrote about it in his famous book, Elements. This book was the first to clearly explain geometry in a step-by-step way.
In Elements, Euclid started with a few basic ideas called axioms. These axioms are like rules that everyone agrees are true without needing proof. From these simple rules, Euclid then showed how to prove many other important ideas, called theorems.
Later, in the 19th century, mathematicians discovered other types of geometry. These are known as non-Euclidean geometry. Scientists like Carl Friedrich Gauss, János Bolyai, and Nikolai Ivanovich Lobachevsky helped create these new ideas. Often, these new geometries change just one of Euclid's original rules, especially the one about parallel lines.
Contents
Euclid's Basic Rules (Axioms)
Euclid's geometry is built on five main assumptions, or axioms. These are ideas that are accepted as true without needing to be proven. They are the starting points for everything else.
Connecting Points with Lines
- Any two points can be connected by a single straight line. Imagine two dots on a paper; you can always draw one straight line between them.
Extending Lines Forever
- Any straight line segment can be made longer forever in a straight direction. So, a short line can become an infinitely long straight line.
Drawing Circles
- You can draw a circle if you know its center and its radius. The radius is a straight line segment from the center to any point on the circle.
Right Angles Are Equal
- All right angles (angles that are exactly 90 degrees) are the same size. No matter where or how you draw them, they will always be equal.
The Parallel Rule
- This is the most famous axiom. It says: If two lines cross a third line, and the angles on one side add up to less than two right angles (less than 180 degrees), then those two lines will eventually meet if you extend them far enough on that side. This rule helps define what parallel lines are.
Images for kids
-
René Descartes. Portrait after Frans Hals, 1648.
-
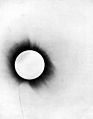
A disproof of Euclidean geometry as a description of physical space. In a 1919 test of the general theory of relativity, stars (marked with short horizontal lines) were photographed during a solar eclipse. The rays of starlight were bent by the Sun's gravity on their way to Earth. This is interpreted as evidence in favor of Einstein's prediction that gravity would cause deviations from Euclidean geometry.
-
The triangle angle sum theorem states that the sum of the three angles of any triangle, in this case angles α, β, and γ, will always equal 180 degrees.
-
A surveyor uses a level
-
Sphere packing applies to a stack of oranges.
-
Geometry is used in art and architecture.
-
The water tower consists of a cone, a cylinder, and a hemisphere. Its volume can be calculated using solid geometry.
-
Geometry can be used to design origami.
See also
In Spanish: Geometría euclidiana para niños
