Non-Euclidean geometry facts for kids

Behavior of lines in different types of geometry

Non-Euclidean geometry is a special kind of geometry. It's different from the normal geometry you might learn in school, which is called Euclidean geometry.

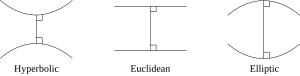
In regular Euclidean geometry, parallel lines never meet. Think of two train tracks that run side-by-side forever. But in Non-Euclidean geometry, parallel lines can actually meet! This happens in two main ways:

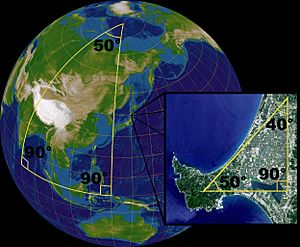
• In elliptic geometry, parallel lines meet at one point. Imagine drawing lines on a ball. Two lines that start parallel at the equator can meet at the North Pole and the South Pole.
• In hyperbolic geometry, parallel lines can meet many, many times.

This idea might seem strange, but it helps us understand shapes and spaces that are not flat, like the surface of a planet.

What Makes It Different?

On a sphere, the angles of a triangle add up to more than 180°.

Non-Euclidean geometry uses different basic rules, called "postulates" or assumptions, compared to Euclidean geometry. For example, one of Euclid's main rules says that through a point not on a line, you can draw only one line parallel to the first line.

In Non-Euclidean geometry, this rule changes:

• In elliptic geometry, you can't draw any parallel lines through that point.
• In hyperbolic geometry, you can draw many parallel lines through that point.

These different rules lead to some surprising results. For instance, in Euclidean geometry, the angles inside any triangle always add up to 180 degrees. But in Non-Euclidean geometry, this isn't always true! On a sphere, the angles of a triangle add up to more than 180 degrees.

How It Started

This type of geometry is called "Non-Euclidean" because it's different from the geometry created by an Ancient Greek mathematician named Euclid. He wrote a famous book called "The Elements" around 300 BC, which laid out the rules for what we now call Euclidean geometry.

For a long time, people thought Euclid's rules were the only way to describe space. But in the 19th century, mathematicians started to wonder what would happen if they changed just one of Euclid's basic rules.

The first people to publish ideas about Non-Euclidean geometry were János Bolyai from Hungary and Nikolai Ivanovich Lobachevsky from Russia. They both wrote about hyperbolic geometry around 1830, working separately. Other smart people, like Carl Friedrich Gauss, had similar ideas even earlier, but they didn't publish their work at the time. Their discoveries showed that there could be other ways to think about space and shapes, opening up new possibilities in mathematics.