Hyperbolic geometry facts for kids
Hyperbolic geometry is a special type of geometry in mathematics. It's different from the normal "Euclidean geometry" you learn in school. The main difference is how it handles parallel lines. In Euclidean geometry, if you have a line and a point not on that line, there's only one line through the point that will never cross the first line. This is called the parallel postulate.
But in hyperbolic geometry, this rule changes! If you have a line and a point not on it, you can draw at least two lines through that point that will never cross the first line. Because of this, hyperbolic geometry is called a "non-Euclidean geometry." Scientists have even built models that show how this works, proving that the parallel postulate is truly different from other geometry rules.
Contents
What Are Non-Crossing Lines?
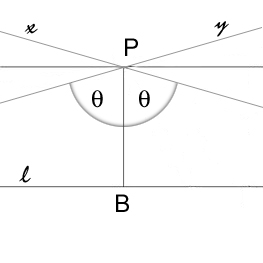
In hyperbolic geometry, lines that don't cross each other can be divided into two main types. Imagine you have a line, let's call it l, and a point P that is not on l.
Asymptotic Lines
If you draw a line from P straight down to l so it makes a perfect corner (90 degrees), let's call that point B. Now, imagine drawing lines from P that get closer and closer to l but never actually touch it. There are two special lines that are the "closest" to l without touching it. These are called asymptotic lines. They get super close to l in one direction but spread far apart in the other.
Ultraparallel Lines
Any other line you draw from P that doesn't cross l (and isn't an asymptotic line) is called ultraparallel. These lines actually get further and further away from l in both directions. There are many, many ultraparallel lines you can draw!
So, in hyperbolic geometry, for any line l and point P not on l:
- There are exactly two lines through P that are asymptotic to l.
- There are an infinite number of lines through P that are ultraparallel to l.
A cool fact about ultraparallel lines is that there's always one unique line that can be drawn perfectly straight across, making a 90-degree angle with both of them.
Angle of Parallelism
In regular Euclidean geometry, the "angle of parallelism" is always 90 degrees, no matter how far apart two parallel lines are. But in hyperbolic geometry, this angle changes! The closer a point is to a line, the more the geometry acts like Euclidean geometry, and the angle of parallelism gets closer to 90 degrees. As the distance gets bigger, the angle gets closer to 0 degrees. This means that on very small scales, it's hard to tell if you're in a Euclidean or hyperbolic world!
History of Hyperbolic Geometry
Many smart people tried to prove the parallel postulate over hundreds of years, including Omar Khayyám and Giovanni Girolamo Saccheri. They didn't succeed in proving it, but their efforts actually helped create the idea of hyperbolic geometry. Some of the earliest ideas came from works by Alhacen and Khayyam.
In the 1800s, two mathematicians, János Bolyai and Nikolai Ivanovich Lobachevsky, independently discovered hyperbolic geometry. Lobachevsky published his work in 1830, and Bolyai published his in 1832. Carl Friedrich Gauss also studied it but didn't publish his findings.
Later, in 1868, Eugenio Beltrami showed how to build models of hyperbolic geometry. This helped prove that if Euclidean geometry was true, then hyperbolic geometry also had to be true. The name "hyperbolic geometry" was first used by Felix Klein in 1871.
Models of the Hyperbolic Plane
To understand hyperbolic geometry better, mathematicians use different "models." These models help us visualize and work with hyperbolic space using ideas from Euclidean geometry.
- Klein Model: This model uses the inside of a circle to represent the hyperbolic plane. Straight lines in this model are shown as straight lines (called "chords") that go from one side of the circle to the other.
- Poincaré Disc Model: This model also uses the inside of a circle. But here, the "straight lines" are parts of circles that meet the edge of the main circle at a 90-degree angle.
- Poincaré Half-Plane Model: This model uses one half of a flat Euclidean plane. The "lines" in this model are either half-circles that stand straight up from the boundary line, or straight lines that are perpendicular to the boundary.
Both Poincaré models are great because they keep the angles the same as they would be in true hyperbolic space.
Visualizing Hyperbolic Geometry
It can be tricky to imagine hyperbolic geometry, but some artists and mathematicians have found cool ways to show it!
M. C. Escher's Art
The famous artist M. C. Escher created prints like Circle Limit III and Circle Limit IV. These artworks show the Poincaré disc model very well. You can see how the shapes get smaller as they move towards the edge of the circle. This helps show how space behaves in hyperbolic geometry.
In these pictures, you might notice that the angles inside triangles (or squares) add up to less than 180 degrees. In regular geometry, they always add up to 180 degrees. This is a key sign of the "negative curvature" of the hyperbolic plane.
Physical Models
You can even make physical models of hyperbolic planes! One famous paper model looks a bit like a trumpet bell and is called a pseudosphere. The art of crochet has also been used to create beautiful, wavy models of hyperbolic planes, like those made by Daina Taimiņa. There's even a "hyperbolic soccerball" made from paper that shows how this geometry works.
Images for kids
-
A hypercycle and pseudogon in the Poincaré disk model.
-
An apeirogon and a horocycle in the Poincaré disk model.
-
The "hyperbolic soccerball" is a paper model that shows part of the hyperbolic plane.
See also
In Spanish: Geometría hiperbólica para niños
