Imaginary unit facts for kids
The imaginary unit, often called i, is a special number in math. It helps us solve problems that don't have answers using only real numbers.
Think of it this way: what number, when multiplied by itself, gives you -1? Normally, you can't find a real number that does this, because any real number multiplied by itself (like 2x2 or -2x-2) always gives a positive result.
Mathematicians created i to be the answer to this problem. So, by definition, i is the square root of -1. This means that i multiplied by i (written as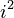 
) equals -1.
The imaginary unit helps us solve equations like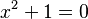 
, which would otherwise have no solution in the world of real numbers. Even though you can't count "i" objects in real life, it's a very useful tool in many areas of science and engineering.
What is the Square Root of i?
You might wonder if you need another special number to find the square root of i. Luckily, you don't! The square roots of i can be written using i itself and real numbers.
The square roots of i are: 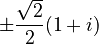Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pm \frac{\sqrt{2}}{2} (1 + i)
This might look a bit complicated, but it just means there are two answers: one positive and one negative. If you were to multiply either of these expressions by itself, the result would be i.
Powers of i
When you multiply i by itself over and over, the answers follow a cool and predictable pattern. Let's look at some examples:
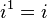(This is just i itself)
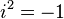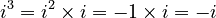
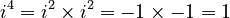
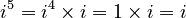
(This is the definition of i)- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): i^3 = i^2 \times i = -1 \times i = -i
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): i^4 = i^2 \times i^2 = -1 \times -1 = 1
- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): i^5 = i^4 \times i = 1 \times i = i
As you can see, the pattern of results is i, -1, -i, 1, and then it repeats! This cycle of four results continues forever.
This repeating pattern means that to find any power of i, you just need to know where it falls in the cycle of four. For example, if you want to find 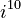Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): i^{10} , you can divide 10 by 4. The remainder tells you where you are in the cycle.
- 10 divided by 4 is 2 with a remainder of 2.
- So, 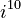Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): i^{10} is the same as 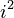, which is -1.
This pattern works for any integer power of i, even negative ones!
Related pages
Images for kids
-
The points (x, y) that make the equation Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1=''xy'' = –1 true form a shape called a hyperbola. This image shows how it looks for an imaginary unit matrix.
