Ramanujan prime facts for kids
A Ramanujan prime is a special type of prime number that follows a rule discovered by the brilliant mathematician Srinivasa Ramanujan. It's connected to how we count prime numbers up to a certain point.
What Are Ramanujan Primes?
In 1919, Ramanujan published an important paper. In it, he proved something related to Bertrand's postulate, which is a statement about prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (like 2, 3, 5, 7, 11).
Ramanujan's work showed a cool pattern about how many prime numbers exist in certain ranges. He looked at the prime counting function, which is written as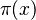 
. This function simply tells you how many prime numbers there are that are less than or equal to a number x. For example, 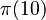Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi(10) is 4, because the primes less than or equal to 10 are 2, 3, 5, and 7.
Ramanujan's discovery was that the number of primes between x/2 and x (which is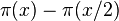 
) is always at least 1, then at least 2, then at least 3, and so on, for all x greater than or equal to certain numbers.
The numbers 2, 11, 17, 29, 41 are the first few Ramanujan primes.
So, a Ramanujan prime, let's call it Rn, is the smallest number that makes sure there are at least n prime numbers between x/2 and x, for every x that is greater than or equal to Rn.
In simpler words, if you pick a Ramanujan prime Rn, you are guaranteed to find at least n prime numbers in the range from half of any number x (where x is bigger than or equal to Rn) up to that number x.
Images for kids
-
A robot thinking about numbers.
