Prime counting function facts for kids
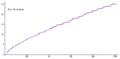
The prime counting function is a special tool in mathematics. It helps us count how many prime numbers there are up to a certain number. We write this function as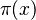 
. It's important to remember that this 
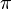has nothing to do with the famous number π (the one used for circles)!
Let's look at some examples:
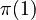- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi(1) is 0, because there are no prime numbers less than or equal to 1.
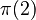- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi(2) is 1, because the only prime number less than or equal to 2 is 2 itself.
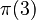- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi(3) is 2, because the prime numbers less than or equal to 3 are 2 and 3.
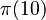- Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi(10) is 4, because the prime numbers less than or equal to 10 are 2, 3, 5, and 7.
.Contents
How the Prime Counting Function Works
The prime counting function, 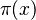, tells you the total number of prime numbers that are less than or equal to a given real number x. For example, if you pick x to be 10, the function counts all primes like 2, 3, 5, and 7. So, 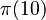Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi(10) equals 4.
If we know the n-th prime number (let's call it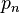 
), then the prime counting function for that number will always be n. For instance, the 5th prime number is 11. So, 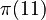Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi(11) equals 5. This means there are exactly 5 prime numbers up to and including 11 (which are 2, 3, 5, 7, and 11).
Why is This Function Important?
The prime counting function is very important in a part of mathematics called number theory. It helps mathematicians understand how prime numbers are spread out among all the other numbers. Prime numbers are like the building blocks of all other numbers, so understanding their distribution is a big deal!
Mathematicians use this function to study patterns and make predictions about primes. Even though primes seem to appear randomly, this function helps reveal some order in their appearance.
Related pages
Images for kids
-
Riemann's explicit formula using the first 200 non-trivial zeros of the zeta function
See also
In Spanish: Función contador de números primos para niños
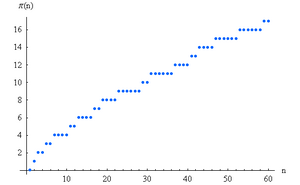
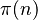