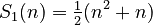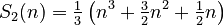Bernoulli number facts for kids
The Bernoulli numbers are a special set of rational numbers (numbers that can be written as a fraction) that show up often in mathematics. They are named after the Swiss mathematician Jacob Bernoulli, who discovered them around the same time as the Japanese mathematician Seki Takakazu.
These numbers are super useful for solving problems, especially when you need to add up powers of numbers. For example, if you want to quickly find the sum of the first 100 numbers squared (1² + 2² + 3² + ... + 100²), Bernoulli numbers can help!
One cool thing about Bernoulli numbers is their pattern:
- Except for the first one, all Bernoulli numbers with an odd number (like B₃, B₅, B₇) are zero.
- For even numbers (like B₂, B₄, B₆), the Bernoulli numbers follow a pattern of positive and negative values. If the number is a multiple of 4 (like B₄, B₈), it's negative. Otherwise, it's positive.
Did you know that Ada Lovelace, often called the first computer programmer, wrote an algorithm (a set of instructions) in 1842 for Charles Babbage's Analytical Engine to calculate Bernoulli numbers? This makes them part of the first complex computer program ever published!
Contents
- History of Bernoulli Numbers
- How Bernoulli Numbers Are Defined
- Bernoulli Numbers and the Riemann Zeta Function
- Computing Bernoulli Numbers Efficiently
- What Are Bernoulli Numbers Used For?
- Connections with Other Math Concepts
- A Visual Way to Understand: The Binary Tree
- Bernoulli Numbers and Pi
- An Algorithmic View: The Seidel Triangle
- Why Are Odd Bernoulli Numbers (Usually) Zero?
- Generalized Bernoulli Numbers
- Images for kids
- See also
History of Bernoulli Numbers
Adding Up Powers: An Ancient Challenge
Mathematicians have always been interested in finding quick ways to add up numbers. Imagine trying to add 1 + 2 + 3 + ... all the way to 100. Or even harder, 1² + 2² + 3² + ... + 100².
Long ago, great thinkers like Pythagoras in Greece, Archimedes in Italy, Aryabhata in India, and Ibn al-Haytham in Iraq worked on these kinds of problems. They found ways to calculate these sums, but their methods were often described in words, not easy formulas.
New Discoveries in Europe
In the 1600s, mathematicians like Thomas Harriot from England, Johann Faulhaber from Germany, and Blaise Pascal from France made big steps forward. Harriot was one of the first to write down formulas using symbols, but he only went up to sums of fourth powers. Faulhaber found formulas for sums up to the 17th power, which was amazing for his time!
But it was Jacob Bernoulli (1654–1705) who first realized there was a single set of special numbers that could help create a general formula for any sum of powers. He was so excited by his discovery that he wrote:
- "With the help of this table, it took me less than half of a quarter of an hour to find that the tenth powers of the first 1000 numbers being added together will yield the sum 91,409,924,241,424,243,424,241,924,242,500."
Bernoulli's work was published after he died, in 1713, in his book Ars Conjectandi. Interestingly, Seki Takakazu in Japan discovered these numbers independently and published his findings a year earlier, in 1712. However, Seki didn't present his method as a general formula based on a sequence of constants like Bernoulli did.
The numbers Bernoulli used in his powerful formula are now known as Bernoulli numbers, a name suggested by Abraham de Moivre.
How Bernoulli Numbers Are Defined
There are several ways to define Bernoulli numbers, but here are three common ones:
Using a Recursive Formula
A recursive formula means you can find the next number in the sequence by using the numbers that came before it. It's like a chain reaction!
For Bernoulli numbers, there are two slightly different versions, usually called B⁻ and B⁺. They are almost the same, except for the first number, B₁. Most modern math books use B⁻, where B₁ = -1/2. Older books, and some mathematicians today, use B⁺, where B₁ = +1/2.
Using an Explicit Formula
An explicit formula lets you calculate any Bernoulli number directly, without needing to know the previous ones. It's like having a direct recipe for each number.
Using a Generating Function
A generating function is a special kind of mathematical expression (like a long polynomial) that "generates" all the Bernoulli numbers as its coefficients. It's a compact way to represent the entire sequence.
Bernoulli Numbers and the Riemann Zeta Function
Bernoulli numbers have a close relationship with another important mathematical concept called the Riemann zeta function. This function is used in many areas of math, including number theory.
You can actually express Bernoulli numbers using the Riemann zeta function. This connection is very important in advanced mathematics and helps mathematicians understand properties of both the Bernoulli numbers and the zeta function.
Computing Bernoulli Numbers Efficiently
Calculating Bernoulli numbers can get very complicated, especially for large numbers. Imagine trying to find B₁₀₀₀₀₀₀! Luckily, mathematicians and computer scientists have found clever ways to compute them much faster.
One method involves calculating the numbers using smaller parts and then combining them. This is similar to how a computer might break down a big problem into smaller, easier ones.
Here's a table showing how far mathematicians have been able to compute Bernoulli numbers over the years:
| Computer | Year | n | Digits |
|---|---|---|---|
| J. Bernoulli | ~1689 | 10 | 1 |
| L. Euler | 1748 | 30 | 8 |
| J. C. Adams | 1878 | 62 | 36 |
| D. E. Knuth, T. J. Buckholtz | 1967 | 1,672 | 3,330 |
| G. Fee, S. Plouffe | 1996 | 10,000 | 27,677 |
| G. Fee, S. Plouffe | 1996 | 100,000 | 376,755 |
| B. C. Kellner | 2002 | 1,000,000 | 4,767,529 |
| O. Pavlyk | 2008 | 10,000,000 | 57,675,260 |
| D. Harvey | 2008 | 100,000,000 | 676,752,569 |
- Digits means how many digits the number has when written out.
What Are Bernoulli Numbers Used For?
Summing Powers of Numbers
This is one of the most important uses of Bernoulli numbers! They help us find a quick formula for the sum of the m-th powers of the first n positive integers. For example, if you want to add up the first n numbers (1 + 2 + ... + n), the formula is:
If you want to add up the squares (1² + 2² + ... + n²), the formula is:
These formulas use Bernoulli numbers as their building blocks. This general formula is often called Faulhaber's formula or Bernoulli's formula.
In Taylor Series
Bernoulli numbers also appear in the Taylor series expansions of many trigonometric functions (like tangent and cotangent) and hyperbolic functions. A Taylor series is a way to represent a function as an infinite sum of terms.
In Topology
Topology is a branch of mathematics that studies shapes and spaces. Bernoulli numbers are used in formulas related to the properties of certain complex shapes, like "exotic spheres." They also appear in the Hirzebruch signature theorem, which is used to understand the structure of smooth, closed shapes in higher dimensions.
Connections with Other Math Concepts
Bernoulli numbers are connected to many other interesting numbers and mathematical ideas.
Worpitzky Numbers
These numbers are defined using factorials and powers. Bernoulli numbers can be found by adding up Worpitzky numbers in a specific way. This shows how Bernoulli numbers are related to a basic counting idea called the inclusion–exclusion principle.
Stirling Numbers
There are two kinds of Stirling numbers, and Bernoulli numbers are linked to both. These connections provide different ways to calculate Bernoulli numbers and show their deep relationships within combinatorics (the study of counting and arrangements).
Pascal's Triangle
Believe it or not, Bernoulli numbers are also connected to Pascal's triangle! You can find a Bernoulli number by calculating the determinant of a special matrix (a grid of numbers) that uses numbers from Pascal's triangle.
Eulerian Numbers
Eulerian numbers are another set of numbers that count specific types of arrangements. Formulas exist that connect Eulerian numbers to Bernoulli numbers, showing more of their hidden relationships.
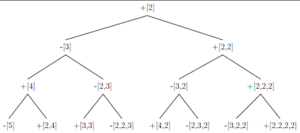
A Visual Way to Understand: The Binary Tree
A mathematician named S. C. Woon found a way to compute Bernoulli numbers using a "binary tree." Imagine a tree where each branch splits into two new branches. By assigning numbers to the "nodes" (points where branches meet) and following certain rules, you can calculate Bernoulli numbers. This gives a visual way to see how these numbers are built.
Bernoulli Numbers and Pi
Bernoulli numbers are also connected to Pi (π), the famous number used to calculate the circumference of a circle. There's a relationship between Bernoulli numbers, Euler numbers (another set of special numbers), and Pi. This connection shows that Pi is deeply rooted in the properties of both Bernoulli and Euler numbers.
An Algorithmic View: The Seidel Triangle
In 1877, Philipp Ludwig von Seidel created a clever algorithm (a step-by-step process) to calculate a sequence of integers called "Euler zigzag numbers." These numbers are directly related to Bernoulli and Euler numbers. Seidel's algorithm involves building a triangle of numbers, where each number is found by adding or subtracting numbers from the previous row. This makes it easier to compute these complex numbers using simple math operations.
Why Are Odd Bernoulli Numbers (Usually) Zero?
You might have noticed that most odd-indexed Bernoulli numbers (like B₃, B₅, B₇, etc.) are zero. This isn't just a coincidence! It's because of some interesting mathematical properties and "combinatorial identities" (ways of counting things) that are hidden within the Bernoulli numbers. When you look at the formulas, these identities cause the terms to cancel out, resulting in zero for odd numbers greater than one.
Generalized Bernoulli Numbers
Just like Bernoulli numbers are related to the Riemann zeta function, there are "generalized Bernoulli numbers" that are related to other special functions called Dirichlet L-functions. These generalized numbers are important in more advanced areas of number theory.
Images for kids
See also
 In Spanish: Número de Bernoulli para niños
In Spanish: Número de Bernoulli para niños