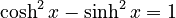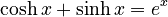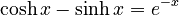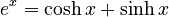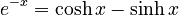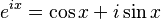Hyperbolic functions facts for kids

Hyperbolic sine (sinh), cosine (cosh), and tangent (tanh).

In mathematics, hyperbolic functions are special functions that are similar to the regular trigonometric functions you might know, like sine and cosine. But instead of being based on a circle, they are based on a hyperbola.

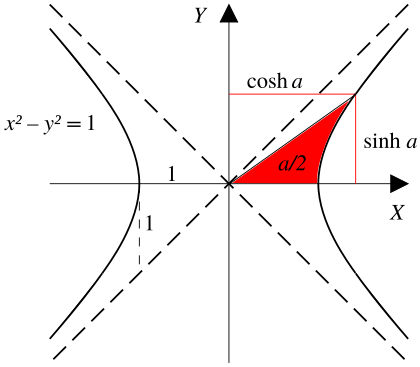
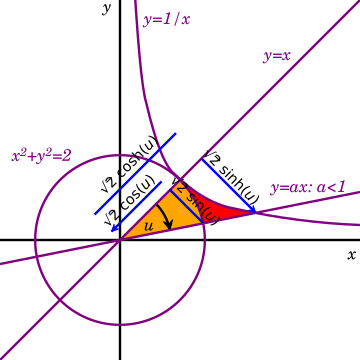
Think of it this way: points on a circle can be described using `(cos t, sin t)`. In the same way, points on a hyperbola can be described using `(cosh t, sinh t)`.

These functions are used in many areas of physics and math. For example, they help solve certain types of differential equations and are important in hyperbolic geometry, which is a different kind of geometry than the one you usually learn.

Meet the Hyperbolic Functions

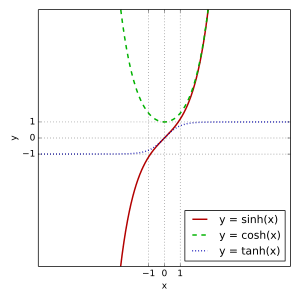
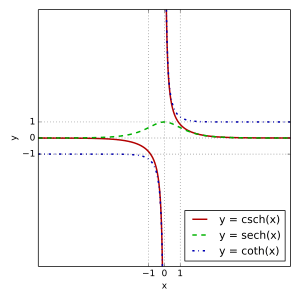
There are six main hyperbolic functions, just like there are six main trigonometric functions.

• Hyperbolic sine (pronounced "sinch" or "shine"), written as sinh
• Hyperbolic cosine (pronounced "kosh"), written as cosh
• Hyperbolic tangent (pronounced "tansh" or "than"), written as tanh
• Hyperbolic cosecant (pronounced "koh-seech" or "koh-shek"), written as csch or cosech
• Hyperbolic secant (pronounced "seech" or "shek"), written as sech
• Hyperbolic cotangent (pronounced "koh-tansh" or "koh-than"), written as coth

There are also inverse hyperbolic functions, which work backward. For example, "arsinh" (or "sinh⁻¹") finds the hyperbolic angle when you know its hyperbolic sine.

This image shows how hyperbolic functions relate to a hyperbola. The value 'a' is twice the area between the ray, the hyperbola, and the x-axis.

These functions take a real number as their input, which is called a hyperbolic angle. The size of this angle is related to the area of a special part of the hyperbola called a hyperbolic sector.

Hyperbolic functions were first introduced by mathematicians Vincenzo Riccati and Johann Heinrich Lambert in the 1760s.

How Hyperbolic Functions are Defined

You can think of hyperbolic functions in a few ways. One common way is using the exponential function, which is `e` raised to a power.

sinh, cosh and tanh functions.

csch, sech and coth functions.

Using Exponential Functions

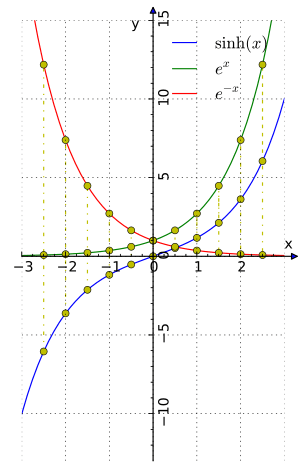
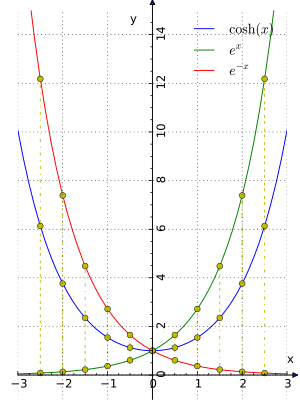
The most basic hyperbolic functions, sinh and cosh, are defined using the exponential function `e^x` and `e^-x`.

• Hyperbolic sine (sinh):

* This is half the difference between `e^x` and `e^-x`. * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sinh x = \frac {e^x - e^{-x}} {2}

The graph of sinh x is half the difference between e^x and e^−x.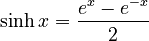

• ^{Hyperbolic cosine (cosh):}

^{* This is the average (or half the sum) of `e^x` and `e^-x`. * 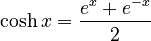Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cosh x = \frac {e^x + e^{-x}} {2}}

^{The graph of cosh x is the average of ex and e−x.}

^{From these two, the others are found:}

• ^{Hyperbolic tangent (tanh):}

^{* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tanh x = \frac{\sinh x}{\cosh x} = \frac {e^x - e^{-x}} {e^x + e^{-x}}}

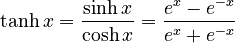
• ^{Hyperbolic cotangent (coth): (for `x` not equal to 0)}

^{* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \coth x = \frac{\cosh x}{\sinh x} = \frac {e^x + e^{-x}} {e^x - e^{-x}}}

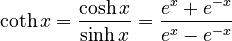
• ^{Hyperbolic secant (sech):}

^{* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \operatorname{sech} x = \frac{1}{\cosh x} = \frac {2} {e^x + e^{-x}}}

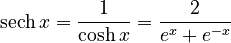
• ^{Hyperbolic cosecant (csch): (for `x` not equal to 0)}

^{* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \operatorname{csch} x = \frac{1}{\sinh x} = \frac {2} {e^x - e^{-x}}}

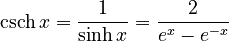
^{Useful Rules and Relations}

^{Hyperbolic functions have many rules, or "identities," that are very similar to the rules for regular trigonometric functions.}

^{Odd and Even Functions}

^{Some functions are "even" (meaning `f(-x) = f(x)`) and some are "odd" (meaning `f(-x) = -f(x)`).}

• ^{`sinh (-x) = -sinh x` (sinh is an odd function)}
• ^{`cosh (-x) = cosh x` (cosh is an even function)}

^{Because of this:}

• ^{`tanh (-x) = -tanh x` (odd)}
• ^{`coth (-x) = -coth x` (odd)}
• ^{`sech (-x) = sech x` (even)}
• ^{`csch (-x) = -csch x` (odd)}

^{Key Identities}

^{One of the most important rules for hyperbolic sine and cosine is:}

• ^{Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cosh^2 x - \sinh^2 x = 1}

^{This is very similar to the famous trigonometric identity `cos^2 x + sin^2 x = 1`.}

^{Other useful rules include:}

• ^{Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cosh x + \sinh x = e^x}
• ^{Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cosh x - \sinh x = e^{-x}}

^{Comparing with Circular Functions}

^{This diagram shows how circular functions (like sine and cosine) relate to a circle, and hyperbolic functions relate to a hyperbola. Both depend on an "area" value.}

^{Hyperbolic functions expand on the idea of trigonometry. Regular trigonometric functions are based on a unit circle, while hyperbolic functions are based on a unit hyperbola.}

^{Both types of functions depend on an "angle" or a value related to an area. For a circle, the area of a sector helps define the circular angle. For a hyperbola, the area of a hyperbolic sector helps define the hyperbolic angle.}

^{Connection to the Exponential Function}

^{The exponential function `e^x` can be split into its "even" and "odd" parts. When you do this, you get the hyperbolic cosine (the even part) and the hyperbolic sine (the odd part)!}

• ^{Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^x = \cosh x + \sinh x}
• ^{Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{-x} = \cosh x - \sinh x}

^{This is similar to Euler's formula for complex numbers, which connects the exponential function to regular sine and cosine:}

• ^{Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{ix} = \cos x + i\sin x}

^{See also}

^{In Spanish: Función hiperbólica para niños}