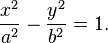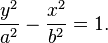Hyperbola Facts for Kids

A hyperbola is the intersection between both halves of a double cone and a plane.

The Brasilia Cathedral has white structures that are shaped like hyperbolas.

A hyperbola is a special kind of curve you might learn about in math class. It's one of the shapes called a conic section. Imagine you have a cone (like an ice cream cone, but with another cone upside down on top of it). If you slice through both parts of this double cone with a flat plane, the shape you get is a hyperbola.

This slice creates two separate curves that look exactly alike. They open in opposite directions. This happens when the angle of the slice is just right – it has to be less steep than the side of the cone itself.

You can find hyperbolas in nature and everyday life. For example, if an object travels in space around another object but never comes back (like a comet that just passes by), it might follow a hyperbolic path. Also, on a sundial, the path the tip of a shadow makes over time can be a hyperbola.

A common example of a hyperbola in math is the graph of the equation f(x) = 1/x.

What Makes a Hyperbola?
Equations of a Hyperbola
Hyperbolic Paths in Space
Images for kids
See also

What Makes a Hyperbola?

This image shows a hyperbola (red curves). The blue dashed lines are the asymptotes. The center is C, and the two vertices are at -a and a. The foci are F₁ and F₂.

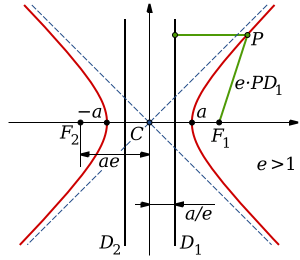
A hyperbola is made of two separate curves. These are called its arms or branches.

The two points where the branches are closest to each other are called the vertices. Imagine a straight line connecting these two points. This line is called the transverse axis. The middle point of this transverse axis is the center of the hyperbola.

As the branches of a hyperbola stretch out far from the center, they get closer and closer to two straight lines. These lines are called asymptotes. The hyperbola will get incredibly close to these asymptotes but will never actually touch or cross them.

There's also a line called the conjugate axis. This line is at a right angle (90 degrees) to the transverse axis.

Equations of a Hyperbola

If a hyperbola's center is at the origin (the point (0,0)) on a Cartesian coordinate system, and its transverse axis is along the x-axis, its equation looks like this:

\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1.

In this equation:

a is the distance from the center to a vertex. The total length of the transverse axis is 2a.
b is related to how wide the hyperbola opens. The length of the conjugate axis is 2b.

This type of hyperbola opens to the left and right. If the hyperbola opens up and down, and its transverse axis is along the y-axis, then its equation changes slightly to:

\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1.

Hyperbolic Paths in Space

A hyperbolic trajectory is the path an object takes when it's moving so fast that it can escape the pull of gravity from a planet, moon, or star. This means its orbital eccentricity (a measure of how stretched out its orbit is) is greater than 1.

For example, some meteors that come from deep space might approach Earth on a hyperbolic path, meaning they just swing by and keep going. Also, space probes that travel to other planets often leave Earth on a hyperbolic path to get enough speed to escape Earth's gravity.