Euler's formula facts for kids
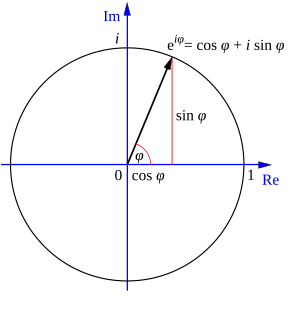
Euler's formula is a very important equation in mathematics. It links exponential functions with trigonometric functions like sine and cosine. This formula is especially useful when working with complex numbers. It was discovered by a famous mathematician named Leonhard Euler in 1748.
The formula looks like this: 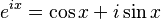
Here's what the different parts mean:
- e is a special number called Euler's number. It's about 2.71828.
- i is the imaginary unit. It's a special number where i squared equals -1 (i.e.,
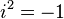 ).
). - x is an angle measured in radians.
- cos x is the cosine of the angle x.
- sin x is the sine of the angle x.
When Euler first shared this formula, he thought x had to be a real number. But later, mathematicians found out that the formula also works even if x is a complex number!
Why is Euler's Formula Important?
Euler's formula is super useful because it connects two big areas of math: exponentials and trigonometry. This connection helps scientists and engineers solve many problems.
For example, it's used in:
- Electrical engineering: To understand how AC circuits work.
- Physics: To describe waves and vibrations.
- Signal processing: To analyze sound and image data.
It also helps us understand Euler's identity, which is often called "the most beautiful equation in mathematics."
Special Cases of the Formula
Euler's formula can show some amazing things when we use specific angles for x.
- When x is π (pi):
If we set x to 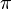 (which is about 3.14159 radians, or 180 degrees), the formula becomes:
(which is about 3.14159 radians, or 180 degrees), the formula becomes: 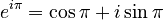 Since
Since 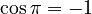 and
and 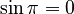 , this simplifies to:
, this simplifies to: 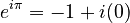
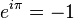 This is known as Euler's identity. It beautifully connects five fundamental numbers in mathematics: e, i,
This is known as Euler's identity. It beautifully connects five fundamental numbers in mathematics: e, i, 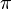 , 1, and 0.
, 1, and 0.
- When x is 2π (two pi):
If we set x to 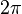 (which is 360 degrees, a full circle), the formula becomes:
(which is 360 degrees, a full circle), the formula becomes: 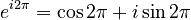 Since
Since 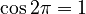 and
and 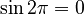 , this simplifies to:
, this simplifies to: 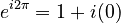
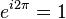 This shows that going a full circle with i in the exponent brings you back to 1.
This shows that going a full circle with i in the exponent brings you back to 1.
See also
 In Spanish: Fórmula de Euler para niños
In Spanish: Fórmula de Euler para niños