Leonhard Euler facts for kids
Quick facts for kids
Leonhard Euler
|
|
|---|---|
Portrait by Jakob Emanuel Handmann (1753)
|
|
| Born | 15 April 1707 Basel, Swiss Confederacy
|
| Died | 18 September 1783 (aged 76) [OS: 7 September 1783] |
| Alma mater | University of Basel (MPhil) |
| Known for |
|
| Spouse(s) |
Katharina Gsell
(m. 1734; died 1773)Salome Abigail Gsell
(m. 1776) |
| Scientific career | |
| Fields | Mathematics and physics |
| Institutions |
|
| Thesis | Dissertatio physica de sono (Physical dissertation on sound) (1726) |
| Doctoral advisor | Johann Bernoulli |
| Doctoral students | Johann Hennert |
| Other notable students |
|
| Signature | |
 |
|
| Notes | |
|
|
Leonhard Euler (born April 15, 1707 – died September 18, 1783) was a brilliant Swiss mathematician and physicist. He also studied astronomy, geography, logic, and engineering. Euler made huge discoveries in many areas of mathematics. He helped create the fields of graph theory and topology.
Euler introduced many of the math symbols and ways of writing we use today. This includes the idea of a mathematical function like f(x). He also worked on mechanics, how fluids move, optics (the study of light), and even music theory. Many people consider him one of the greatest mathematicians ever. He wrote more than 800 books and papers! He spent most of his adult life in Saint Petersburg, Russia, and Berlin, Prussia.
Contents
Who Was Leonhard Euler?
Leonhard Euler is famous for popularizing the Greek letter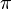 
for the ratio of a circle's circumference to its diameter. He was also the first to use 
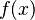for functions. He used the letter 
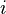for the imaginary unit 
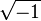. He also used 
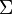for summation and 
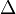for finite differences. He gave us the modern definition of the constant 
, known as Euler's number.
Euler was the first to work on graph theory. He solved the famous Seven Bridges of Königsberg problem. He also discovered that for any polyhedron, the number of corners (vertices) plus the number of flat surfaces (faces) minus the number of edges always equals 2. This is called the Euler characteristic. In physics, he rewrote Newton's laws of motion. This helped explain how solid objects move. He also studied how objects bend and stretch.
Early Life and Learning
Leonhard Euler was born on April 15, 1707, in Basel, Switzerland. His father, Paul III Euler, was a pastor. His mother was Marguerite Brucker. Leonhard was the oldest of four children. His family moved to Riehen, Switzerland, where he spent most of his childhood.
From a young age, Euler learned math from his father. His father had learned from a famous mathematician named Jacob Bernoulli. When Euler was about eight, he went to a Latin school in Basel. He also had a private tutor who was very interested in math.
In 1720, at just 13 years old, Euler started at the University of Basel. This was normal for the time. He took a math class from Johann Bernoulli, Jacob's younger brother. Johann Bernoulli quickly saw how talented Euler was. He advised Euler to read difficult math books and offered to help him with any problems.
Because of Bernoulli's support, Euler's father agreed to let him become a mathematician instead of a pastor. In 1723, Euler earned a degree comparing the ideas of René Descartes and Isaac Newton. He then studied to become a pastor.
In 1726, Euler wrote a paper about how sound travels. He tried to get a job at the University of Basel but didn't succeed. In 1727, he entered a competition held by the French Academy of Sciences. The challenge was to find the best way to place masts on a ship. Euler came in second place. Over his life, he entered this competition 15 times and won 12 of them!
Moving to Saint Petersburg
Johann Bernoulli's sons, Daniel and Nicolaus, went to work at the Imperial Russian Academy of Sciences in Saint Petersburg in 1725. They promised to help Euler get a job there. In 1726, Nicolaus sadly died. Daniel took his brother's place and suggested Euler for his old job in physiology. Euler accepted the offer in November 1726.
Euler arrived in Saint Petersburg in May 1727. He quickly moved to a math position at the academy. He lived with Daniel Bernoulli and they worked closely together. Euler learned Russian and even took a side job as a medic in the Russian Navy.
The academy in Saint Petersburg was created by Peter the Great to improve education in Russia. It attracted many foreign scholars like Euler. However, after Peter the Great's wife, Catherine I, died, Russian nobles gained power. They were suspicious of foreign scientists and cut funding for the academy.
Things got a little better in 1730 when Anna of Russia became empress. Euler quickly became a professor of physics in 1731. He also left the Russian Navy. In 1733, Daniel Bernoulli left Saint Petersburg, and Euler became the head of the math department. In 1734, he married Katharina Gsell.
Life in Berlin
Euler was worried about the ongoing problems in Russia. So, in June 1741, he left Saint Petersburg for a job at the Berlin Academy. Frederick the Great had offered him the position. Euler lived in Berlin for 25 years and wrote hundreds of papers there.
In 1748, his important book on functions, Introductio in analysin infinitorum, was published. In 1755, he published a book on differential calculus. During his time in Berlin, he was chosen as a member of the Royal Swedish Academy of Sciences and the French Academy of Sciences.
Euler also taught Friederike Charlotte of Brandenburg-Schwedt, Frederick's niece. He wrote over 200 letters to her about physics and math. These letters were published as Letters to a German Princess. This book was translated into many languages and became very popular. It showed how well Euler could explain science to people who weren't scientists.
Even though Euler contributed a lot to the Berlin Academy, Frederick II didn't always appreciate him. Frederick saw Euler as a simple, religious man who didn't fit in with the other intellectuals at his court. Euler wasn't good at debates and sometimes argued about things he didn't know much about.
Euler kept a strong connection with the St. Petersburg Academy. He published many papers in Russia and helped Russian students. In 1760, during a war, Russian troops damaged Euler's farm. The Russian empress, Empress Elizabeth, even sent him a large payment to help. Euler decided to leave Berlin in 1766 and return to Russia.
During his years in Berlin (1741–1766), Euler was incredibly productive. He wrote 380 works. He also managed the academy's library, observatory, and botanical garden. He even helped design the water fountains at the King’s palace.
Back to Russia
The political situation in Russia became stable after Catherine the Great became empress. So, in 1766, Euler accepted an invitation to return to the St. Petersburg Academy. He asked for a high salary and pensions for his family. He was helped by his student Anders Johan Lexell. In 1771, a fire destroyed Euler's home in St. Petersburg.
His Family Life
On January 7, 1734, Euler married Katharina Gsell. She was the daughter of a painter from the Academy. They bought a house by the Neva River. They had thirteen children, but only five lived past childhood: three sons and two daughters. Their first son was Johann Euler, who also became a mathematician.
After Katharina died in 1773, Euler married her half-sister, Salome Abigail Gsell, in 1776. This marriage lasted until his death in 1783. His brother, Johann Heinrich, also moved to St. Petersburg in 1735 and worked as a painter at the academy.
His Amazing Eyesight Story
Euler's eyesight got worse throughout his life. In 1738, he became almost blind in his right eye. He thought it was because of the map-making work he did for the St. Petersburg Academy. Even in Germany, his vision in that eye got worse. Frederick II even called him "Cyclops." But Euler said, "Now I will have fewer distractions."
In 1766, he got a cataract in his left eye. An operation helped for a short time, but he eventually became almost totally blind in that eye too. However, his blindness didn't stop him. With the help of his assistants, Euler's work actually increased! In 1775, he wrote about one math paper every week.
His Final Years
On September 18, 1783, in St. Petersburg, Euler had lunch with his family. He was talking about the newly discovered planet Uranus and its orbit with his student Lexell. Then, he suddenly collapsed and died from a brain hemorrhage.
Euler was buried next to his first wife, Katharina. In 1957, his tomb was moved to the Lazarevskoe Cemetery at the Alexander Nevsky Monastery.
What Euler Gave Us: Math and Science
Euler worked in almost every area of mathematics. This included geometry, calculus, trigonometry, algebra, and number theory. He also worked on physics, the lunar theory (study of the Moon's motion), and other science fields. He is a very important person in the history of math. His works, if printed, would fill 60 to 80 large books! Some people say he was responsible for a third of all scientific and mathematical discoveries in the 18th century.
New Ways to Write Math
Euler created and made popular many of the math symbols we use in textbooks today. Most importantly, he introduced the idea of a function. He was the first to write f(x) to show a function f applied to a value x. He also introduced the modern way of writing trigonometric functions. He used the letter e for the base of the natural logarithm, now called Euler's number. He also used the Greek letter Σ for sums and the letter i for the imaginary unit. Euler also helped make the Greek letter π popular for the ratio of a circle's circumference to its diameter.
Numbers and Their Secrets
Euler was very interested in number theory. He built on the work of another mathematician, Pierre de Fermat. Euler proved some of Fermat's ideas and showed that some of his guesses were wrong. For example, Fermat thought that all numbers of a certain form were prime, but Euler proved this wasn't true.
Euler found a link between how prime numbers are spread out and other math ideas. He proved that if you add up the reciprocals of all prime numbers, the sum keeps growing forever. He also found a connection between the Riemann zeta function and prime numbers.
Euler invented the totient function, which counts how many positive numbers less than or equal to a number n don't share any common factors with n. He used this to make Fermat's little theorem more general, creating what is now called Euler's theorem. He also made big contributions to the study of perfect numbers. He proved a special relationship between even perfect numbers and Mersenne primes. Euler's ideas helped pave the way for the work of Carl Friedrich Gauss, another famous mathematician. By 1772, Euler had proved that a very large number, 231 − 1, was a Mersenne prime. This was the largest known prime for a long time.
Solving Puzzles with Graphs
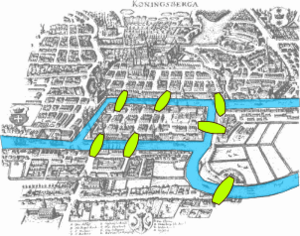
In 1735, Euler solved a famous puzzle called the Seven Bridges of Königsberg. The city of Königsberg had two islands in a river, connected to each other and the mainland by seven bridges. The puzzle was to find a path that crossed each bridge exactly once and ended where it started. Euler proved that it was impossible. This solution is considered the very first theorem in graph theory.
Euler also discovered a formula for convex polyhedrons: the number of vertices (corners) minus the number of edges plus the number of faces (flat surfaces) always equals 2. This formula,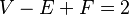 
, is now known as the Euler characteristic. Studying and expanding this formula led to the field of topology, which is about shapes and spaces.
Physics, Space, and Building Things
Euler was very good at solving real-world problems using math. He used his skills to apply Leibniz's differential calculus and Newton's ideas to physical problems. He also found ways to make better guesses for solving math problems, inventing what are now called Euler approximations.
Euler helped create the Euler–Bernoulli beam equation, which is very important in structural engineering. He also used his math skills to study problems in space. He won many awards for his work in astronomy. He could figure out the orbits of comets and other space objects very accurately. His calculations helped create better longitude tables for navigation.
Euler made important contributions to optics, the study of light. He disagreed with Newton's idea that light was made of tiny particles. Euler's papers helped make the wave theory of light (that light travels in waves) the main idea for a long time.
In fluid dynamics, Euler was the first to predict cavitation in 1754. This is when bubbles form in a liquid due to pressure changes. The Euler number, used in fluid flow calculations, comes from his work on how efficient turbines are. In 1757, he published important equations for how fluids flow without friction, known as the Euler equations.
Euler is also well-known in structural engineering for his formula that tells engineers how much weight a column can hold before it bends or buckles.
Logic and Diagrams
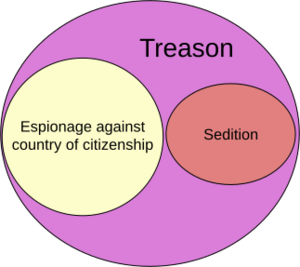
Euler is known for using closed curves to show how ideas relate in logic (1768). These drawings are now called Euler diagrams.
An Euler diagram uses simple closed curves, usually circles, to show sets and how they relate to each other. Each curve divides the space into two parts: the inside, which represents the elements in the set, and the outside, which represents everything not in the set. The size or shape of the curves doesn't matter. What matters is how they overlap.
If two curves don't cross, it means the sets have no common elements. If they do cross, the area where they overlap shows the elements that are in both sets. If one curve is completely inside another, it means one set is a subset of the other. Euler diagrams are used to help visualize different combinations of characteristics.
Math and Music
One of Euler's unique interests was using math ideas in music. In 1739, he wrote a book called Attempt at a New Theory of Music. He hoped to make music theory a part of mathematics. However, this work wasn't widely known. Some said it was too mathematical for musicians and too musical for mathematicians.
Euler's approach to music was mostly mathematical. For example, he used binary logarithms to describe how octaves are divided into smaller parts. His writings on music were not many, but they show an interest that stayed with him throughout his life.
How He is Remembered
.jpg)
Euler's picture has been on Swiss 10-franc banknotes. He has also appeared on many Swiss, German, and Russian postage stamps. In 1782, he was chosen as an honorary member of the American Academy of Arts and Sciences. An asteroid, 2002 Euler, was named after him.
Images for kids
-
Euler's signature
-
Euler's grave at the Alexander Nevsky Monastery
See also
In Spanish: Leonhard Euler para niños
