Seven Bridges of Königsberg facts for kids

A map of Königsberg from Euler's time, showing the Pregel River and its seven bridges.

The Seven Bridges of Königsberg is a very famous problem in mathematics. A brilliant mathematician named Leonhard Euler solved it in 1735. His solution helped create a new area of math called graph theory. This also helped develop another math field called topology.

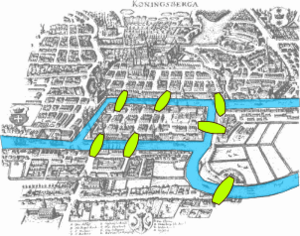
The city of Königsberg (which is now Kaliningrad, Russia) was built on both sides of the Pregel River. It had two big islands. These islands were connected to each other and to the main land by seven bridges.

The puzzle was to find a way to walk through the city. You had to cross each of the seven bridges exactly one time. You could not cross any bridge more than once. You also could not reach the islands without using the bridges. The walk did not have to start and end in the same place. Euler proved that there was no way to do this walk.

Why This Problem Is Important

Euler's solution to the Königsberg bridge problem is a big deal in the history of mathematics. It is seen as the very first idea in graph theory. Graph theory is a part of math that studies how things are connected. It is now often considered a branch of combinatorics, which is about counting and arranging things.

What Happened to the Bridges?

Over time, the original seven bridges of Königsberg changed. Two of them were destroyed during the bombing of Königsberg in World War II. Later, two more bridges were taken down. A modern highway was built in their place.

Three of the original bridges still exist today. However, only two of these three are truly from Euler's time. One of them was rebuilt in 1935. So, by the year 2000, there were five bridges in Kaliningrad.

In terms of graph theory, it is now possible to walk across all the bridges exactly once. This is because the way the bridges are connected has changed. But this special walk would have to start on one island and end on the other. This makes it not very useful for people visiting the city.

Related Pages

• Hamiltonian path
• Travelling salesman problem

Images for kids

• 

  A modern map of Kaliningrad. The bridges that are still there are shown in green. The ones that were destroyed are shown in red.

• 

  This picture shows the Königsberg Cathedral. The bridge on the right is one of the two bridges that are still standing from Euler's time.

See also

In Spanish: Problema de los puentes de Königsberg para niños