Hamiltonian path facts for kids
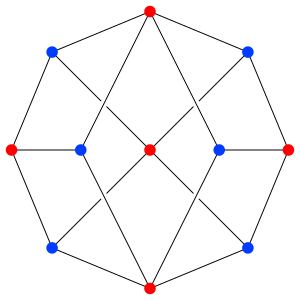
A Hamiltonian path is a special kind of journey you can take through a network, or "graph." Imagine a map with cities and roads connecting them. A Hamiltonian path visits every single city exactly once. If this path also starts and ends in the same city, making a complete loop, it's called a Hamiltonian cycle.
Finding these paths and cycles is a big challenge in graph theory, which is a branch of mathematics. It's much harder than finding an Eulerian path, which only needs to use every road exactly once. The problem of finding a Hamiltonian path is known as "NP-complete," which means it's very difficult for computers to solve quickly, especially for large networks.
Networks can be either directed or undirected. In a directed network, roads might be one-way streets, meaning you can only travel in one direction. In an undirected network, roads are two-way, so you can travel in both directions. A famous real-world example of this problem is the Travelling Salesman Problem. Here, the goal is to find the shortest Hamiltonian cycle, often in a directed network, where each road has a "weight" or "distance" attached to it.
Who Discovered Hamiltonian Paths?
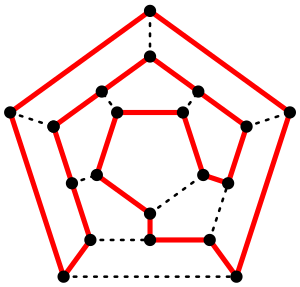
These paths and cycles are named after William Rowan Hamilton, a famous mathematician. In 1857, he invented a game called the Icosian game, also known as Hamilton's puzzle.
Hamilton's Puzzle
Hamilton's puzzle involved finding a Hamiltonian cycle on the edges of a dodecahedron. A dodecahedron is a 3D shape with 12 flat faces, each a pentagon. Imagine its edges as roads and its corners as cities. Hamilton found a way to visit every corner exactly once and return to the start.
While Hamilton made these paths famous, another mathematician named Thomas Kirkman had actually studied Hamiltonian cycles in polyhedra a year earlier, in 1856.
Images for kids
-
A Hamiltonian cycle around a network of six vertices (points).
See also
In Spanish: Camino hamiltoniano para niños
