William Rowan Hamilton facts for kids
Quick facts for kids
Sir William Rowan Hamilton
|
|
|---|---|
Sir William Rowan Hamilton (1805–1865)
|
|
| Born | 4 or 3 August 1805 Dublin, Ireland
|
| Died | 2 September 1865 (aged 60) Dublin, Ireland
|
| Nationality | British (United Kingdom of Great Britain and Ireland) |
| Alma mater | Trinity College Dublin |
| Known for | Hamilton's principle Hamiltonian mechanics Hamiltonians Hamilton–Jacobi equation Quaternions Biquaternions Hamiltonian path Icosian calculus Nabla symbol Versor Coining the word 'tensor' Coining the word 'scalar' cis notation Hamiltonian vector field Icosian game Universal algebra Hodograph Hamiltonian group Cayley–Hamilton theorem |
| Spouse(s) | Helen Maria Bayly |
| Children | William Edwin Hamilton, Archibald Henry Hamilton, Helen Eliza Amelia O'Regan, née Hamilton |
| Awards | Royal Medal (1835) Cunningham Medal (1834 and 1848) |
| Scientific career | |
| Fields | Mathematics, astronomy, physics |
| Institutions | Trinity College, Dublin |
| Academic advisors | John Brinkley |
| Influences | Zerah Colburn John T. Graves |
| Influenced | Peter Guthrie Tait |
Sir William Rowan Hamilton (born August 3 or 4, 1805 – died September 2, 1865) was a brilliant Irish mathematician, astronomer, and physicist. He held important positions at Trinity College Dublin, including Andrews Professor of Astronomy and Royal Astronomer of Ireland. He lived at Dunsink Observatory.
Hamilton's scientific work covered many areas. He studied how light behaves (geometrical optics) and worked on complex math ideas like Fourier analysis. His most famous work was on quaternions, which helped create modern linear algebra. He made big contributions to optics, classical mechanics (how things move), and abstract algebra (a type of math). His ideas were very important for theoretical physics, especially his new way of looking at Newtonian mechanics, now called Hamiltonian mechanics. This work is still key in understanding things like electricity and magnetism, and quantum mechanics (how tiny particles behave).
Contents
Early Life and Amazing Talents
William Rowan Hamilton was the fourth of nine children. His parents were Sarah Hutton and Archibald Hamilton. They lived in Dublin, Ireland. When William was just three years old, he went to live with his uncle, James Hamilton. His uncle was a graduate of Trinity College Dublin and ran a school in Trim, County Meath.
William showed incredible talent from a very young age. His uncle noticed that William was amazing at learning languages. By age seven, he was already good at Hebrew. Before he turned 13, he had learned about a dozen languages! These included classical languages, modern European languages, and even languages like Persian, Arabic, Hindustani, and Sanskrit. His father wanted him to work for the British East India Company, which is why languages were so important.
Young William was also a fantastic mental calculator. He could quickly figure out math problems with many decimal places. In 1813, a nine-year-old American math genius named Zerah Colburn visited Dublin. William, who was eight, competed against him in a mental math contest. Colburn won easily.
After this defeat, William spent less time on languages and more on mathematics. At ten, he found a Latin copy of Euclid's geometry book. At twelve, he studied Newton's Arithmetica Universalis. He then read Newton's famous Principia. By age 16, he had mastered much of it, along with other advanced math topics. He even thought he found a mistake in the work of a famous mathematician named Laplace. This led him to meet John Brinkley, who was the Royal Astronomer of Ireland.
Student Years and Big Achievements
In 1822, Hamilton began to deeply study Laplace's Mécanique Céleste (a book on celestial mechanics). By the end of that year, he had written his first three original math papers. He showed two of them to Brinkley, who was very impressed. In 1823, at age 18, William got into Trinity College Dublin. His tutor, Charles Boyton, introduced him to new math ideas from Paris. John Brinkley said of the young Hamilton, "This young man, I do not say will be, but is, the first mathematician of his age."
Hamilton got top grades in every subject and every exam at college. He was expected to win many student awards. However, his college career was cut short in a surprising way. In 1826, Brinkley left his job to become a bishop. Even though Hamilton was still a student, he was chosen in 1827 to take over Brinkley's important roles. He became the Andrews Professor of Astronomy and the Royal Astronomer of Ireland.
Life at Dunsink Observatory
As the Royal Astronomer of Ireland, Hamilton moved into Dunsink Observatory. He lived and worked there for the rest of his life, from 1827 until his death in 1865. In his early years at Dunsink, he regularly observed the stars and planets. His assistant, Charles Thompson, handled the routine observations. Hamilton's sisters also helped with the observatory's work.
Hamilton's astronomy lectures were very popular. Not only his students, but also scholars, poets, and women came to listen. A poet named Felicia Hemans even wrote a poem called The Prayer of the Lonely Student after hearing one of his lectures.
Travels and Poetic Friends
In 1827, Hamilton invited his four sisters, including the poet Eliza Mary Hamilton, to live with him at the observatory. They managed his household until he married in 1833.
Hamilton traveled around Ireland and England with Alexander Nimmo, who taught him about latitude and longitude. During one trip, he visited the famous poet William Wordsworth at his home in Rydal Mount. Hamilton sent many poems to Wordsworth and became a "poetic disciple."
When Wordsworth visited Dublin in 1829, he stayed with Hamilton at Dunsink. On another trip to England in 1831, Hamilton met up with Wordsworth again in the Lake District. Hamilton also visited another famous poet, Samuel Taylor Coleridge, in 1832.
Family Life
In 1833, Hamilton married Helen Marie Bayly, who was the daughter of a country preacher. They had three children: William Edwin Hamilton (born 1834), Archibald Henry (born 1835), and Helen Elizabeth (born 1840). Helen was often ill, which made family life challenging at times.
Later Life and Death
Hamilton remained sharp and focused until his last days. He spent his final six years working on a book called Elements of Quaternions. He died on September 2, 1865, after a severe attack of gout. He is buried in Mount Jerome Cemetery in Dublin.
Physics Discoveries
Hamilton made very important contributions to how we understand optics (the study of light) and classical mechanics (the study of motion).
His first major discovery was in a paper he wrote in 1823. In 1827, he presented a new idea called Hamilton's principal function. This single function brought together the theories of mechanics and optics. It helped build the foundation for the wave theory of light in mathematical physics. He even predicted a new phenomenon called conical refraction. This is where a ray of light entering a special crystal at a certain angle comes out as a hollow cone of rays.
Hamilton's work on "Varying Action" was a big step. He applied his ideas from optics to dynamics (the study of forces and motion). This led to his famous papers in 1834 and 1835.
Why Hamilton's Work Was Important
Hamiltonian mechanics was a powerful new way to solve problems about motion. Hamilton's ideas made it possible to solve many more complex mechanical problems. His "Varying Action" principle was based on earlier work by other scientists. However, Hamilton found a deeper mathematical structure. He showed a special balance between momentum and position.
Both Hamilton's and Lagrangian mechanics (another important approach) are still used today. They are key to studying continuous systems in physics, like electromagnetism, quantum mechanics, and relativity theory. Many scientists have built upon Hamilton's work, showing how important his ideas were and still are.
Mathematics Breakthroughs
Hamilton's math studies were unique and developed without much help from others. His writings didn't belong to any specific school of thought. He was given the freedom to advance science in the best way he could.
Quaternions: A New Kind of Number
Hamilton made his famous discovery of quaternions in 1843. He was trying to find a way to extend complex numbers (which can be thought of as points on a 2-dimensional graph) into higher dimensions. He found the solution by working with four dimensions instead of three.
According to Hamilton, on October 16, 1843, he was walking along the Royal Canal in Dublin with his wife. Suddenly, the key equation for quaternions came to him:
- i2 = j2 = k2 = ijk = −1
He was so excited that he carved this equation into the side of the nearby Broom Bridge with his penknife!
Quaternions were revolutionary because they meant giving up the commutative law (where a x b = b x a). This was a very bold step at the time. Hamilton also introduced the ideas of the cross product and dot product for vectors. He even invented the words "tensor" and "scalar" and was the first to use the word "vector" in its modern sense.
Other Math Work
Hamilton also studied how to solve complex equations, like the solution of the quintic. He looked into "fluctuating functions" in Fourier analysis and invented the hodograph (a diagram used in mechanics).
He also created the icosian game, also known as Hamilton's puzzle. This game is based on finding a Hamiltonian path in graph theory.
Awards and Recognition
Hamilton received the Cunningham Medal from the Royal Irish Academy twice. He won the first award in 1834 for his work on conical refraction. The next year, he also received the Royal Medal from the Royal Society for the same discovery. He won the Cunningham Medal again in 1848.
In 1835, he was knighted by the Lord Lieutenant of Ireland during a meeting of the British Association for the Advancement of Science in Dublin. Many other honors followed quickly. In 1837, he was elected president of the Royal Irish Academy. He also became a special corresponding member of the Saint Petersburg Academy of Sciences. Later, in 1864, the new United States National Academy of Sciences put Hamilton's name at the top of their list of first Foreign Associates.
Hamilton's Lasting Legacy
A special plaque under the Broom Bridge, where Hamilton carved his quaternion equation, was put up in 1958. Since 1989, the National University of Ireland, Maynooth, organizes a "Hamilton Walk" every year. Mathematicians walk from Dunsink Observatory to the bridge to remember his discovery.
The Hamilton Institute at Maynooth University is an applied mathematics research center named after him. The Royal Irish Academy also holds an annual public Hamilton lecture. In 2005, the 200th anniversary of his birth, the Irish government called it Hamilton Year, celebrating Irish science. Trinity College Dublin opened the Hamilton Mathematics Institute that year.
Ireland issued two commemorative stamps in 1943 to mark 100 years since he announced quaternions. In 2005, the Central Bank of Ireland released a 10-euro silver coin to celebrate his 200th birthday.
Things Named After Hamilton
- Hamilton's equations: A way to describe motion in classical mechanics.
- Hamilton's principle and the Hamilton–Jacobi equation are also named after him.
- The Hamiltonian: This is a name for a special function in physics (classical and quantum mechanics) and also a term in graph theory.
- The algebra of quaternions is often written as H or
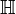to honor Hamilton. - The Hamilton Building at Trinity College Dublin is named after him.
Hamilton in Literature
Some modern mathematicians have suggested that Charles Lutwidge Dodgson (who wrote Alice in Wonderland as Lewis Carroll) might have made fun of Hamilton's work on quaternions in his book. They thought the Mad Hatter's tea party might represent the idea that quaternions were silly. However, in 2022, new evidence was presented that suggests this idea might be based on a misunderstanding of quaternions and their history.
Images for kids
-
Master Noakes, a mental calculator, 1827 lithograph
See also
In Spanish: William Rowan Hamilton para niños
- List of astronomers
- List of things named after William Rowan Hamilton
- Theoretical physics
Sources
- Chow, Tai L. (2013). Classical Mechanics: Chaper 5: Hamilton Formulation of Mechanics: Description of Motion in Phase Spaces. CRC Press, ISBN: 978-1466569980
