Classical mechanics facts for kids

Diagram of orbital motion of a satellite around the earth, showing perpendicular velocity and acceleration (force) vectors.

In physics, classical mechanics is a big part of how we understand motion. It's all about the rules that describe how objects move when forces act on them. This field of study is very old and important in science and engineering. You might also hear it called Newtonian mechanics, named after Isaac Newton.

Classical mechanics helps us understand how large objects move. This includes everything from a thrown projectile (like a baseball) to parts of machinery. It also explains the movement of huge objects in space, like spacecraft, planets, stars, and even galaxies.

This field works really well for big objects and speeds that are not super fast. But when objects are very tiny, like atoms and molecules, we need a different kind of physics called quantum mechanics. And for tiny, super-fast objects, we use quantum field theory.

The name classical mechanics was first used in the early 1900s. It describes the ideas about physics that Isaac Newton and other scientists developed in the 1600s. It also builds on earlier ideas from Johannes Kepler about how planets move. Classical mechanics uses simple ideas about how matter and forces work. It assumes that objects have clear properties, like their exact location and speed.

Newton's Three Laws of Motion
Kinematic Equations
- 1-Dimensional Kinematics
- 2-Dimensional Kinematics
  - X-Direction Equations
  - Y-Direction Equations
Branches of Classical Mechanics
Related pages
Images for kids
See also

Newton's Three Laws of Motion

A page from Newton's book about the three laws of motion

Isaac Newton created three very important laws about motion. These laws are key to classical mechanics.

The First Law says that an object will stay still or keep moving at the same speed in a straight line unless a force pushes or pulls on it. Before Newton, people thought things just stopped if no force was present. A common way to say this is: Objects that are stopped tend to stay stopped, and objects that are moving tend to stay moving, unless an outside force acts on them.

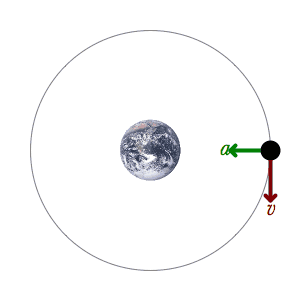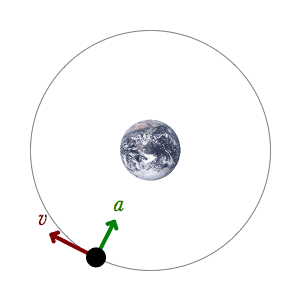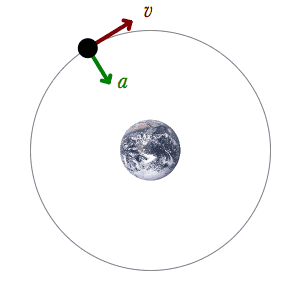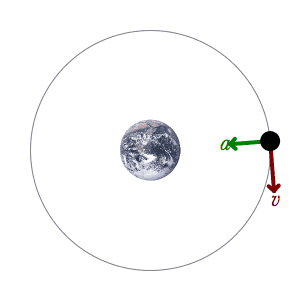
The Second Law explains how a force makes something move. It says that the total force on an object changes its momentum. Simply put, a bigger force makes an object speed up more, or a heavier object needs a bigger force to speed up the same amount.

The Third Law states that for every action, there is an equal and opposite reaction. This means if you push on something, that something pushes back on you with the same amount of force. For example, if you jump forward off a boat, the boat moves backward.

Kinematic Equations

In physics, kinematics is a part of classical mechanics. It describes how objects move without worrying about why they move or what effects their movement has.

1-Dimensional Kinematics

1-Dimensional (1D) Kinematics is used when an object moves only in one direction. This could be side to side (left or right) or up and down. There are equations you can use to solve problems about movement in just one dimension. These equations come from the basic ideas of velocity, acceleration, and distance.

The first 1D kinematic equation connects acceleration and velocity. It's used when acceleration and velocity don't change.

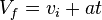
Equation: $V_f=v_i+at$

V_f is the final velocity (how fast it's going at the end).

v_i is the starting or initial velocity (how fast it was going at the start).

a is the acceleration (how much its speed changes per second).

t is time (how long the object was accelerating).

The second 1D kinematic equation helps find the distance an object moved. It uses the average velocity and the time.

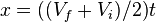
Equation: $x=((V_f+V_i)/2)t$

x is the distance moved.

V_f is the final velocity.

v_i is the starting or initial velocity.

t is time.

The third 1D kinematic equation finds the distance traveled while an object is accelerating. It uses velocity, acceleration, time, and distance.

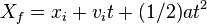
Equation: $X_f=x_i+v_it+(1/2)at^2$

$X_f$ is the final distance from a starting point.

x_i is the starting or initial distance.

v_i is the starting or initial velocity.

a is the acceleration.

t is time.

The fourth 1D kinematic equation finds the final velocity. It uses the initial velocity, acceleration, and distance traveled.

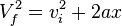
Equation: $V_f^2=v_i^2+2ax$

V_f is the final velocity.

v_i is the starting or initial velocity.

a is the acceleration.

x is the distance moved.

2-Dimensional Kinematics

2-Dimensional (2D) kinematics is used when an object moves in two directions at once. For example, it might move both left-to-right (x-direction) and up-and-down (y-direction). There are different equations for each direction. Galileo showed that movement in the x-direction doesn't affect movement in the y-direction. However, the y-direction is affected by gravity, so its speed changes.

X-Direction Equations

Movement left and right

The main x-direction equation is used because the velocity (speed and direction) in the x-direction usually stays the same.

Equation: $X=V_x*t$

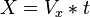
X is the distance moved in the x-direction.

V_x is the velocity in the x-direction.

t is time.

Y-Direction Equations

Movement up and down. This is affected by gravity or other forces.

The first y-direction equation is like the first 1D equation, but it focuses on the changing y-velocity. It's used for objects falling freely due to gravity.

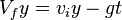
Equation: $V_fy=v_iy-gt$

V_fy is the final y-velocity.

v_iy is the starting or initial y-velocity.

g is the acceleration due to gravity, which is about 9.8 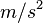$m/s^2$ (meters per second squared) or 32 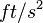$ft/s^2$ (feet per second squared).

t is time.

The second y-direction equation is used when an object is affected by an acceleration other than gravity.

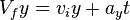
Equation: $V_fy=v_iy+a_yt$

V_fy is the final y-velocity.

v_iy is the starting or initial y-velocity.

a_y is the acceleration in the y-direction.

t is the time.

The third y-direction equation finds the distance moved in the y-direction. It uses the average y-velocity and the time.

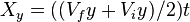
Equation: $X_y=((V_fy+V_iy)/2)t$

X_y is the distance moved in the y-direction.

V_fy is the final y-velocity.

v_iy is the starting or initial y-velocity.

t is the time.

The fourth y-direction equation deals with distance moved in the y-direction while affected by gravity.

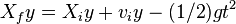
Equation: $X_fy=X_iy+v_iy-(1/2)gt^2$

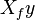$X_fy$ is the final distance moved in the y-direction.

x_iy is the starting or initial distance in the y-direction.

v_iy is the starting or initial velocity in the y-direction.

g is the acceleration of gravity (9.8 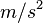$m/s^2$ or 32 $ft/s^2$ ).

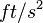t is time.

The fifth y-direction equation deals with distance moved in the y-direction while affected by an acceleration other than gravity.

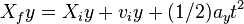
Equation: $X_fy=X_iy+v_iy+(1/2)a_yt^2$

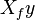$X_fy$ is the final distance moved in the y-direction.

x_iy is the starting or initial distance in the y-direction.

v_iy is the starting or initial velocity in the y-direction.

a_y is the acceleration in the y-direction.

t is time.

The sixth y-direction equation finds the final y-velocity when gravity acts over a certain distance.

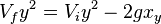
Equation: $V_fy^2=V_iy^2-2gx_y$

V_fy is the final velocity in the y-direction.

V_iy is the starting or initial velocity in the y-direction.

g is the acceleration of gravity (9.8 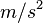$m/s^2$ or 32 $ft/s^2$ ).

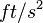x_y is the total distance moved in the y-direction.

The seventh y-direction equation finds the final y-velocity when another acceleration acts over a certain distance.

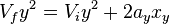
Equation: $V_fy^2=V_iy^2+2a_yx_y$

V_fy is the final velocity in the y-direction.

V_iy is the starting or initial velocity in the y-direction.

a_y is the acceleration in the y-direction.

x_y is the total distance moved in the y-direction.

Branches of Classical Mechanics

Classical mechanics is often divided into different areas of study:

Statics: This is the study of objects that are not moving, or are in balance. It looks at the forces acting on them.
Dynamics: This branch studies motion and how it relates to the forces that cause it.
Kinematics: As we learned, this deals with describing motion itself, without looking at what caused it.

Other ways to divide classical mechanics include:

Celestial mechanics: This is the study of how stars, planets, and other space objects move.
Continuum mechanics: This looks at materials that can be thought of as continuous, like solids, liquids, and gases.
Relativistic mechanics: This is for objects moving at speeds close to the speed of light, using ideas from Einstein's theories of relativity.
Statistical mechanics: This connects the tiny movements of individual atoms and molecules to the larger, overall properties of materials, like their temperature or pressure.

Newton's laws of motion

Images for kids

Sir Isaac Newton (1643–1727) was a key figure in physics. His three laws of motion are the foundation of classical mechanics.
Lagrange helped explain Newton's ideas using advanced mathematics, which is now called Lagrangian mechanics.
Hamilton further developed Lagrangian mechanics, creating what is now known as Hamiltonian mechanics.