Quantum field theory facts for kids
In theoretical physics, quantum field theory (QFT) is a special way of thinking about how the universe works. It combines three big ideas: classical field theory (which describes forces like electricity and magnetism), special relativity (about space and time at high speeds), and quantum mechanics (about tiny particles).
QFT helps us understand subatomic particles, like electrons and photons. It says that particles are actually just "bumps" or "excited states" in invisible fields that fill all of space. Imagine a calm ocean; a particle is like a wave or ripple on that ocean. The ocean itself (the field) is more fundamental than the waves (the particles).
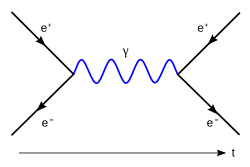
When particles interact, it's like their fields are "talking" to each other. Scientists use special drawings called Feynman diagrams to help visualize and calculate these interactions.
Contents
History of Quantum Field Theory
Quantum field theory has a long history, developed by many smart scientists throughout the 20th century. It started in the 1920s when physicists wanted to describe how light and electrons interact. This led to the first quantum field theory, called quantum electrodynamics (QED).
But there was a big problem: calculations in QFT often led to answers that were "infinity"! It was like trying to count to the end of numbers. This problem was finally solved in the 1950s with a clever trick called renormalization.
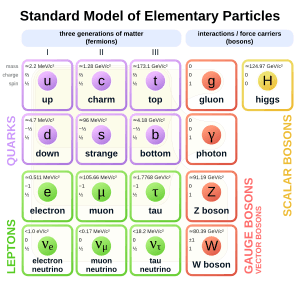
Later, QFT struggled to explain other forces, like the weak interaction and strong interaction. Some scientists even thought about giving up on QFT. But then, new ideas like gauge theory came along. By the 1970s, QFT was back, leading to the creation of the Standard Model of particle physics, which describes almost all known particles and forces.
Early Ideas About Fields
To understand QFT, let's look at some older ideas it built upon.
Long ago, people like Isaac Newton thought gravity was an "action at a distance"—meaning objects pulled on each other instantly, no matter how far apart. But Newton himself found this hard to imagine.
Later, in the 18th century, scientists found it easier to describe gravity using the idea of a "field." A field is like an invisible influence that fills space. For gravity, it's a number (or direction and strength) at every point in space that tells you how gravity would affect a particle there. At first, this was just a mathematical trick.
Fields became more "real" with the study of electromagnetism in the 19th century. Michael Faraday introduced the idea that electric and magnetic fields are physical properties of space itself. He said that interactions happen through these fields, not instantly across distances.
James Clerk Maxwell completed the theory of classical electromagnetism in 1864 with his famous Maxwell's equations. These equations showed that electric and magnetic fields could travel as waves at the speed of light. This proved that "action at a distance" was wrong.
From Classical to Quantum
Even with the success of electromagnetism, it couldn't explain everything. For example, it couldn't explain why atoms only emit light at specific colors (atomic spectra) or how hot objects glow (blackbody radiation).
Max Planck started quantum mechanics by studying blackbody radiation. He suggested that energy isn't continuous; it comes in tiny, discrete packets, or "quanta." Imagine a ramp versus stairs; energy is like stairs.
Building on this, Albert Einstein proposed in 1905 that light itself is made of these energy packets, which he called photons. So, light acts like both a wave (in the electromagnetic field) and a particle (photons).
In 1913, Niels Bohr showed that electrons in atoms also have discrete energy levels. This was another example of "quantization." Then, Louis de Broglie suggested that all tiny particles have both wave-like and particle-like properties. These ideas came together to form quantum mechanics in the mid-1920s.
Around the same time, Einstein also published his theory of special relativity. This theory changed how we think about space and time, especially for objects moving very fast. It said that physical laws must be the same for all observers, no matter their speed.
But there were still problems. Quantum mechanics couldn't explain why atoms sometimes spontaneously emit light without any outside push. Also, it didn't fit well with special relativity.
The Birth of Quantum Electrodynamics (QED)
Since the electromagnetic field was the only known field in the 1920s, scientists started by trying to "quantize" it. This means turning the classical electromagnetic field into a quantum field.
In 1927, Paul Dirac created quantum electrodynamics (QED). He added a term to the theory that described how electric currents interact with the electromagnetic field. QED successfully explained why atoms spontaneously emit light. It said that even in empty space (a vacuum), there are tiny, constant jitters in the electromagnetic field, called quantum fluctuations. These jitters "stimulate" electrons to emit light.
Dirac also wrote an equation in 1928 that described fast-moving electrons. This equation had some strange results, like suggesting there were "negative energy states." To fix this, Dirac and others realized these negative energy states actually meant there were particles with the same mass as electrons but opposite charge. This was the first idea of antimatter! In 1932, the positron (the antimatter partner of the electron) was discovered in cosmic rays. This showed that particles could be created or destroyed, which QFT naturally explains.
The Problem of Infinities and Renormalization
Even with QED's successes, a major problem remained. When scientists tried to do more detailed calculations (called "higher-order perturbative calculations"), they kept getting infinite answers. It was like the math was breaking down. For example, the calculated "self-energy" of an electron (its energy due to its own field) was infinite.
Many physicists were frustrated. Some even suggested giving up on QFT. But in the late 1940s and early 1950s, a breakthrough happened. Scientists like Julian Schwinger, Richard Feynman, Freeman Dyson, and Shin'ichirō Tomonaga developed a systematic way to remove these infinities. This method is called renormalization.
The main idea of renormalization is that the "bare" mass and charge of a particle (the ones in the equations) are not what we actually measure. The measured mass and charge are already affected by the particle's interactions with its own field. Renormalization allows us to replace the infinite "bare" values with the finite, measured values. This made QED calculations match experiments incredibly well, solving the "war against infinities."
Around the same time, Feynman introduced Feynman diagrams. These are simple drawings that help visualize and calculate particle interactions. Each line and point in a diagram represents a mathematical term, making complex calculations much easier to organize.
The Standard Model
After QED's success, physicists wanted to apply QFT to other forces. In 1954, Yang Chen-Ning and Robert Mills developed a new type of gauge theory called Yang-Mills theory. This theory was more complex than QED but could describe particles that themselves carry a "charge" for the force.
In the 1960s, Sheldon Glashow, Abdus Salam, and John Clive Ward used these ideas to create a theory that unified the electromagnetic force and the weak interaction into a single "electroweak" force. However, this theory also had problems with infinities.
Then, in 1964, Peter Higgs and others proposed a mechanism called spontaneous symmetry breaking. This idea suggested that particles that were originally massless could gain mass by interacting with a special field, now known as the Higgs boson.
In 1971, Gerard 't Hooft proved that Yang-Mills theories could be "renormalized," meaning their infinities could be removed. This was a huge step! Steven Weinberg then combined the electroweak theory with the Higgs mechanism, and it worked.
Soon after, scientists like Harald Fritzsch, Murray Gell-Mann, and Heinrich Leutwyler developed quantum chromodynamics (QCD) to describe the strong interaction, the force that holds atomic nuclei together. They discovered that the strong force gets weaker at very high energies, a property called "asymptotic freedom." This meant that QFT could finally make predictions for the strong force too.
These breakthroughs led to the creation of the Standard Model of elementary particles. The Standard Model successfully describes all known fundamental forces except gravity. Its predictions have been confirmed by many experiments, including the discovery of the Higgs boson at CERN in 2012.
QFT in Other Areas
Even though QFT started with particle physics, it's also very useful in other areas, especially in condensed matter physics. This field studies how large groups of atoms behave, like in solids and liquids.
For example, the idea of the Higgs mechanism (how particles get mass) actually came from studying superconductors. Also, the concept of renormalization was inspired by studying how materials change their properties at certain temperatures (phase transitions).
QFT helps describe "quasiparticles" in materials. These aren't real particles, but they act like particles and help explain how energy moves through a material. For example, "phonons" are quasiparticles that describe vibrations in a crystal.
How Quantum Field Theory Works (Simplified)
Let's try to understand the core ideas of QFT without getting lost in complex math.
Classical Fields Revisited
Imagine a classical field, like the gravitational field around Earth or the electric field around a charged object. It's like an invisible influence that spreads throughout space. At every point, the field has a value that tells you how strong the force would be there. These fields can change over time.
But classical fields can't explain everything, like why light comes in discrete packets (photons). QFT takes this idea of a field and gives it quantum properties.
Quantizing Fields
In QFT, we "quantize" these classical fields. Think of it like this:
- A classical field is like a smooth, continuous wave on a pond.
- When we quantize it, it's like saying the wave can only exist in specific, discrete "chunks" of energy. These chunks are the particles.
So, instead of thinking of particles as tiny balls, QFT sees them as excited states or "quanta" of their underlying fields.
- The electron field exists everywhere. An electron is an excitation of the electron field.
- The photon field exists everywhere. A photon is an excitation of the photon field.
This means particles can be created or destroyed. If you put enough energy into a field, you can create a new "bump" or particle. If a particle loses energy, it can disappear back into the field. This is why particle numbers aren't fixed in high-energy interactions.
Feynman Diagrams: Visualizing Interactions
When particles interact, it's like their fields are exchanging energy. Feynman diagrams are simple drawings that help us understand and calculate these interactions.
Each line in a Feynman diagram represents a particle moving through space and time. A point where lines meet (a "vertex") represents an interaction. For example, in quantum electrodynamics (QED), an electron might emit a photon. This would be shown as an electron line bending and a photon line coming off it.
These diagrams help physicists calculate the "scattering amplitude"—the probability that a certain interaction will happen. They are a powerful tool for making predictions that can be tested in experiments.
Renormalization: Taming Infinities
As mentioned before, early QFT calculations often gave infinite answers, which didn't make sense. Renormalization is the process that fixes this.
Imagine you're trying to measure the mass of an electron. The "bare" electron (the one in the equations) is constantly interacting with its own field, even in empty space. These interactions add an infinite amount to its mass. Renormalization says: "We can't measure the 'bare' mass. We only measure the 'physical' mass, which already includes all these interactions."
So, instead of trying to calculate the infinite "bare" mass, we use the finite mass we measure in experiments. We adjust the terms in our equations so that the final calculated results match what we observe. This process allows us to get meaningful, finite answers from theories that would otherwise give infinities.
Some theories are "renormalizable," meaning we can always get rid of the infinities by adjusting a few basic properties like mass and charge. The Standard Model is a renormalizable theory. Other theories are "non-renormalizable," meaning new infinities appear at every step, and we can't fix them all. This often means the theory is only useful at low energies and needs a more complete theory at higher energies.
Running Coupling Constants
One cool idea from renormalization is the "running coupling constant." This means the strength of a force isn't always the same; it changes depending on the energy scale of the interaction.
For example, in QED, the electromagnetic force (carried by photons) actually gets stronger at very high energies. But in quantum chromodynamics (QCD), the strong interaction (carried by gluons) gets weaker at high energies. This is "asymptotic freedom," and it's why quarks inside protons and neutrons are tightly bound at low energies but act almost free at very high energies.
Gauge Symmetry: The Hidden Rules
Many QFTs have a special property called gauge symmetry. This means that you can make certain mathematical changes to the fields in the theory without changing any of the physical predictions. It's like having different ways to describe the same thing.
For example, in QED, the way we describe the electromagnetic field can be changed in a specific way (a "gauge transformation"), but the actual electric and magnetic fields we measure remain the same. This symmetry is not just a mathematical trick; it's deeply connected to fundamental laws. Noether's theorem says that every continuous symmetry leads to a conservation law. For example, the gauge symmetry in QED leads to the conservation of electric charge.
Spontaneous Symmetry Breaking: How Particles Get Mass
Spontaneous symmetry breaking is a fascinating idea where the laws of physics (the Lagrangian) might have a certain symmetry, but the actual state of the universe (the vacuum) doesn't show that symmetry.
Imagine a perfectly round bowl with a marble at the very top. The bowl is symmetrical. But if the marble rolls down, it will settle at some point on the rim, breaking the perfect symmetry of the top.
In particle physics, this idea is crucial for the Higgs mechanism. The fundamental fields in the Standard Model are initially massless due to gauge symmetry. But then, they interact with the Higgs boson field, which has a non-zero value everywhere in space. This interaction "breaks" the symmetry and gives other particles, like the W and Z bosons and quarks, their mass. The Higgs boson itself is an excitation of this Higgs field.
Supersymmetry: A Future Idea?
Scientists are always looking for new ideas beyond the Standard Model. One such idea is supersymmetry. This theory suggests that every known particle (like electrons and photons) has a "superpartner" with a different spin. For example, the superpartner of an electron (a fermion) would be a "selectron" (a boson).
If supersymmetry is real, it could solve some big problems in physics, like why the Higgs boson has the mass it does, or what dark matter is made of. However, no superpartner particles have been found yet. If they exist, they must be very heavy, meaning our current experiments aren't powerful enough to create them.
Images for kids
-
Magnetic field lines visualized using iron filings. When a piece of paper is sprinkled with iron filings and placed above a bar magnet, the filings align according to the direction of the magnetic field, forming arcs.
See also
 In Spanish: Teoría cuántica de campos para niños
In Spanish: Teoría cuántica de campos para niños