Maxwell's equations Facts for Kids

Maxwell's equations are a set of four important rules that explain how electric charges and electric currents create electric fields and magnetic fields. They also describe how these fields can create each other! Think of them as the basic laws of electromagnetism, which is the study of electricity and magnetism working together.

In the 1860s, a smart scientist named James Clerk Maxwell put these ideas together. His equations, along with another rule called the Lorentz force equation, help us understand how tiny charged particles move when they are in electric and magnetic fields. These rules are super important for understanding almost all modern technology!

The first rule helps us figure out the electric field made by an electric charge. The second rule helps us understand magnetic fields. The other two rules describe how fields "circulate" or loop around their sources. For example, magnetic fields can loop around electric currents or changing electric fields. This is part of Ampère's law. Also, electric fields can loop around changing magnetic fields, which is explained by Faraday's law.

The Four Big Ideas of Maxwell's Equations
Why Maxwell's Equations Are Important
Images for kids
See also

The Four Big Ideas of Maxwell's Equations

Maxwell's equations are usually written using complex math, but their main ideas are quite simple to understand. They tell us four key things about electricity and magnetism:

1. Electric Fields Come from Charges

This idea is called Gauss's law for electricity. It tells us that electric charges create electric fields. Imagine an electric charge, like a tiny electron. It creates an invisible electric field around it, which can push or pull other charges. The more charge you have, the stronger the electric field will be.

2. Magnetic Fields Don't Have Single Poles

This is called Gauss's law for magnetism. It means you can never find a single "north" magnetic pole without a "south" pole, or vice versa. Magnets always have both a north and a south pole. If you break a magnet in half, you don't get a separate north pole and a separate south pole; you just get two smaller magnets, each with its own north and south pole!

3. Changing Magnetic Fields Make Electric Fields

This idea is known as Faraday's law. It explains how a changing magnetic field can create an electric field. This is how electric generators work! When a magnet moves near a coil of wire, the changing magnetic field makes electrons in the wire move, creating an electric current. This is also how things like wireless chargers work.

4. Electric Currents and Changing Electric Fields Make Magnetic Fields

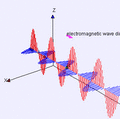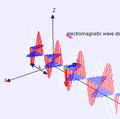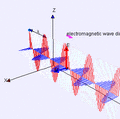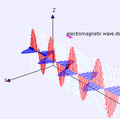
This is Ampère's law (with Maxwell's important addition). It tells us that electric currents (moving charges) create magnetic fields around them. This is how electromagnets work. Maxwell added that a changing electric field can also create a magnetic field. This tiny but crucial addition showed that light itself is an electromagnetic wave, made of electric and magnetic fields dancing together!

Why Maxwell's Equations Are Important

These four equations are incredibly important because they explain how electricity and magnetism are connected and how they work together. They showed that light is an electromagnetic wave, meaning it's made of vibrating electric and magnetic fields. This discovery led to understanding radio waves, microwaves, X-rays, and all other forms of electromagnetic radiation.

Thanks to Maxwell's equations, we have:

Radio and television
Cell phones and Wi-Fi
Electric power grids
Radar and GPS
And countless other technologies that rely on electricity and magnetism!

They are a cornerstone of modern physics and engineering, helping us design everything from tiny computer chips to huge power plants.

Images for kids

In a geomagnetic storm, a surge in the flux of charged particles temporarily alters Earth's magnetic field, which induces electric fields in Earth's atmosphere, thus causing surges in electrical power grids. (Not to scale.)
Magnetic-core memory (1954) is an application of Ampère's law. Each core stores one bit of data.
This 3D diagram shows a plane linearly polarized wave propagating from left to right. The oscillating fields are detected at the flashing point. The horizontal wavelength is λ.