Differential calculus Facts for Kids

Differential calculus, a part of calculus, is a way to study how things change. Imagine you're watching a car. Differential calculus helps you figure out its exact speed at any moment, not just its average speed. It's like finding out how steep a curve is at a single point, even though the curve is always bending.

This powerful math tool helps us understand how one thing changes when another thing changes. It was created in the late 1600s by two brilliant minds, Sir Isaac Newton and Gottfried Leibniz.

Understanding Change
- Slopes and Curves
How Differential Calculus Works
Differentiation Rules
Related pages
Images for kids
See also

Understanding Change

Think about things that change, like distance and time. In a running race, a runner's distance from the start line keeps growing. At the same time, a stopwatch measures how much time passes.

We can easily find the average speed of the runner. You just divide the total distance by the total time. But what if you want to know the runner's exact speed at 1.5 seconds into the race? The average speed won't tell you that.

Before calculus, people tried to find this exact speed by looking at smaller and smaller time periods. They would calculate the average speed over a tiny fraction of a second. This was a very long and hard process. It had to be done over and over for each new problem. It's like trying to guess a car's speed using only its odometer and a clock, without a speedometer!

Slopes and Curves

On a curve, the steepness changes. The red and blue lines are tangents. They show the exact steepness at those points.

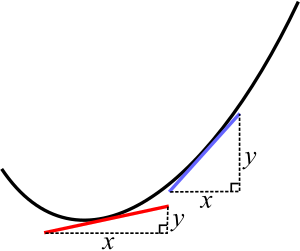
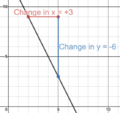
Another similar problem is finding the steepness of a curve at any point. For a straight line, finding the slope is easy. You just see how much it goes up (the 'y' change) and divide it by how much it goes across (the 'x' change). If a straight line goes from (2,10) to (4,18), it goes up 8 and across 2. So, its slope is 8 divided by 2, which is 4.

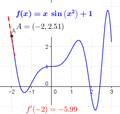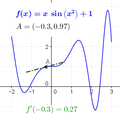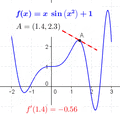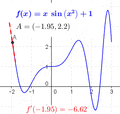
But a curve is different because it bends. Its steepness changes at every point. If you zoom in very, very close on a tiny part of a curve, it looks almost like a short straight line. To find its slope, you can draw a straight line that just touches the curve at that one point. This special line is called a tangent. It has the exact same steepness as the curve at that point.

The challenge was knowing if the tangent line was exactly right. Our eyes aren't precise enough to be sure.

Newton and Leibniz found a way to calculate this exact steepness (or speed). They imagined dividing the curve into an endless number of super tiny pieces. They looked at points very, very close to the one they cared about. As these points got closer, the slope they calculated got closer and closer to a specific value. They realized this specific value was the true slope at that exact point.

How Differential Calculus Works

Let's use a math example. Imagine a function like y = f(x). This means the value of 'y' depends on the value of 'x'. For example, if we have the equation y = x², then if x is 1, y is 1 (1x1). If x is 3, y is 9 (3x3).

This picture shows two points on a curve: 'x' and 'x + h'. 'h' is a tiny distance between them.

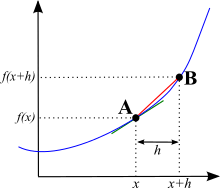
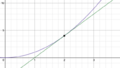
Pick a point A on the curve. Let its horizontal position be x. Now, pick another point B, just a tiny bit further along the curve. Let its horizontal position be x + h. Here, 'h' is a very, very small number.

When we move from point A to point B, the vertical position changes from f(x) to f(x + h). The horizontal position changes from x to x + h.

Remember, slope is "how much it goes up" divided by "how much it goes across." So, the slope between A and B is: 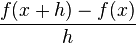$\frac{f(x + h) - f(x)}{h}$

Now, imagine point B getting closer and closer to point A. This means 'h' gets closer and closer to 0. As 'h' approaches 0, we get closer to knowing the exact slope at point A. This idea of getting "closer and closer" is called a limit: 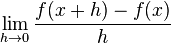$\lim_{h\rightarrow0} \frac{f(x + h) - f(x)}{h}$

Let's try this with our example, y = x². 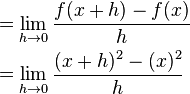$\begin{align} &= \lim_{h\rightarrow0} \frac{f(x+h) - f(x)}{h} \\ &= \lim_{h\rightarrow0} \frac{(x+h)^2 - (x)^2}{h} \end{align}$ Using a math rule called the binomial theorem (which says (x+h)² = x² + 2xh + h²), we can simplify this: 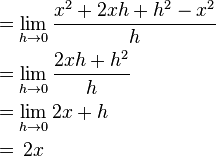$\begin{align} &= \lim_{h\rightarrow0} \frac{x^2 + 2xh + h^2 - x^2}{h} \\ &= \lim_{h\rightarrow0} \frac{2xh + h^2}{h} \\ &= \lim_{h\rightarrow0} 2x + h \\ &= \frac{}{} 2x \end{align}$ So, for the curve f(x) = x², the exact steepness (or derivative) at any point is 2x. This process of finding the slope using limits is called differentiation. The derivative is often written as f'(x) (with an apostrophe).

Leibniz used a slightly different way to write this. He called 'h' "dx" (meaning a tiny change in x). He called the resulting change in f(x) "dy" (meaning a tiny change in y). Leibniz's way of writing it, 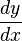$\frac{dy}{dx}$ , is very common because it's clear when equations get more complex. It means "the change in y divided by the change in x."

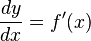
$\frac{dy}{dx} = f'(x)$

Differentiation Rules

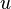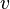Mathematicians have figured out many rules for differentiation. These rules work for all kinds of functions. They make finding derivatives much faster than using the "limit" method every time. (In the table below, $u$ and $v$ are both functions that depend on $x$ ).

Condition	Function	Derivative	Example	Derivative
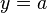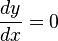A number by itself	$y = a$	$\frac{dy}{dx} = 0$	$y = 3$	$0$
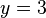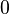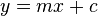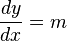A straight line	$y = mx + c$	$\frac{dy}{dx} = m$	$y = 3x + 5$	$3$
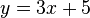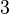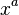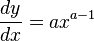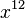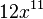x to the power of a number	$x^a$	$\frac{dy}{dx} = a x^{a-1}$	$x^{12}$	$12x^{11}$
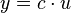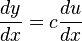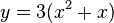A number multiplied by a function	$y = c\cdot u$	$\frac{dy}{dx} = c \frac{du}{dx}$	$y=3(x^2 + x)$	$3(2x + 1)$
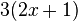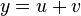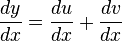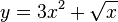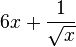A function plus another function	$y = u + v$	$\frac{dy}{dx} = \frac{du}{dx} + \frac{dv}{dx}$	$y = 3x^2 + \sqrt{x}$	$6x + \frac{1}{\sqrt{x}}$
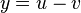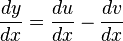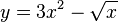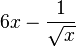A function minus another function	$y = u - v$	$\frac{dy}{dx} = \frac{du}{dx} - \frac{dv}{dx}$	$y = 3x^2 - \sqrt{x}$	$6x - \frac{1}{\sqrt{x}}$
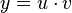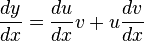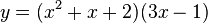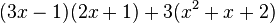Product Rule (One function multiplied by another)	$y = u \cdot v$	$\frac{dy}{dx} = \frac{du}{dx}v + u\frac{dv}{dx}$	$y = (x^2 + x + 2)(3x-1)$	$(3x-1)(2x+1) + 3(x^2+x+2)$
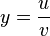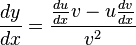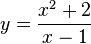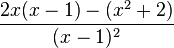Quotient Rule (One function divided by another)	$y = \frac{u}{v}$	$\frac{dy}{dx} = \frac{\frac{du}{dx}v - u\frac{dv}{dx}}{v^2}$	$y = \frac{x^2 + 2}{x-1}$	$\frac{2x(x - 1) - (x^2 + 2)}{(x-1)^2}$
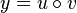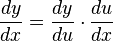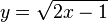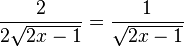Chain rule (For functions inside other functions)	$y = u \circ v$	$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$	$y = \sqrt{2x-1}$	$\frac{2}{2\sqrt{2x-1}} = \frac{1}{\sqrt{2x-1}}$
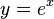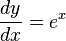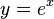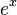An exponential function	$\frac{}{} y = e^x$	$\frac{dy}{dx} = e^x$	$\frac{}{} y = e^x$	$\frac{}{} e^x$

Images for kids

The graph of a function y=f(x). The orange line is tangent to the curve at x=a. This means the straight line and the curve have the same steepness at that exact point.
This animation shows how the tangent line changes as it moves along a curve, showing the steepness at different points.
This is the graph of a straight line.
This is the graph of y=x^2. The straight line shown is tangent to the curve at the point (2,4). The steepness (slope) of this tangent line is 4.
The dotted line goes through two points on the curve y=x^2. When these two points are close, the dotted line's steepness is very similar to the tangent line's steepness. As the points get closer, the difference becomes tiny.

Differential calculus facts for kids

Contents

Understanding Change

Slopes and Curves

How Differential Calculus Works

Differentiation Rules

Related pages

Images for kids

See also