Binomial theorem facts for kids

Kids Encyclopedia Facts

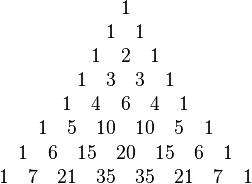
\begin{array}{c} 1 \\ 1 \quad 1 \\ 1 \quad 2 \quad 1 \\ 1 \quad 3 \quad 3 \quad 1 \\ 1 \quad 4 \quad 6 \quad 4 \quad 1 \\ 1 \quad 5 \quad 10 \quad 10 \quad 5 \quad 1 \\ 1 \quad 6 \quad 15 \quad 20 \quad 15 \quad 6 \quad 1 \\ 1 \quad 7 \quad 21 \quad 35 \quad 35 \quad 21 \quad 7 \quad 1 \end{array}

The binomial coefficient

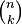\tbinom{n}{k}

appears as the

k

th entry in the

n

th row of Pascal's triangle (counting starts at

0

). Each entry is the sum of the two above it.

The binomial theorem is a cool rule in algebra that helps us expand expressions like $(x + y) n$ . This means multiplying a two-term expression (a "binomial") by itself many times. Instead of doing all the multiplication, the theorem gives us a shortcut!

When you expand $(x + y) n$ , you get a sum of terms like $ax b y c$ . Here, $b$ and $c$ are whole numbers, and their sum $b + c = n$ . The number $a$ in front of each term is called a binomial coefficient. These special numbers can be found in Pascal's triangle. They also tell us how many ways we can choose a certain number of items from a group, which is a big part of combinatorics.

Discovering the Binomial Theorem

People have known about parts of the binomial theorem for a very long time!

Early Discoveries

Around 4th century BC, the Greek mathematician Euclid knew about the binomial theorem for the power of 2. This means he knew that .
Another Greek mathematician, Diophantus, worked with cubes of binomials, like $(n-1) 3$ .
Around 510 CE, the Indian mathematician Aryabhata had a method for finding cube roots. This suggests he understood the binomial formula for the power of 3.

Indian and Persian Contributions

Ancient Indian mathematicians were interested in binomial coefficients. These numbers show how many ways you can pick $k$ objects from a group of $n$ objects without putting them back.
The earliest known mention of this problem is in the Chandaḥśāstra by Pingala (around 200 BC).
By the 6th century AD, Indian mathematicians likely knew how to calculate these coefficients using factorials. A clear rule for this was written in the 12th century by Bhaskara.
The first full explanation of the binomial theorem and a table of binomial coefficients was by Al-Karaji in Persia. He described the triangular pattern (like Pascal's triangle) and even proved the theorem using an early form of mathematical induction.
The Persian poet and mathematician Omar Khayyam probably knew about the formula for higher powers, but many of his math works are lost.

European Developments

In the 13th century, Chinese mathematicians Yang Hui and Chu Shih-Chieh also knew about binomial expansions. Yang Hui said the method came from an even older text by Jia Xian from the 11th century.
In 1544, Michael Stifel used the term "binomial coefficient." He showed how to use Pascal's triangle to expand expressions.
Blaise Pascal studied the triangle in detail in his book Traité du triangle arithmétique. However, other European mathematicians like Stifel, Niccolò Fontana Tartaglia, and Simon Stevin already knew about the number pattern.
Isaac Newton is usually given credit for finding the generalized binomial theorem in 1665. This version works for any type of exponent, not just whole numbers. James Gregory also discovered it on his own in 1670.

What the Binomial Theorem Says

The binomial theorem tells us how to expand $(x + y) n$ when $n$ is a whole number that is zero or greater.

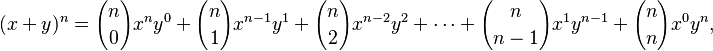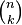It looks like this: $(x+y)^n = {n \choose 0}x^n y^0 + {n \choose 1}x^{n-1} y^1 + {n \choose 2}x^{n-2} y^2 + \cdots + {n \choose n-1}x^1 y^{n-1} + {n \choose n}x^0 y^n,$ Here, $\tbinom nk$ are the binomial coefficients. When an exponent is 0, the term is 1 (like ).

We can write this formula shorter using summation notation: 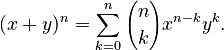Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle (x+y)^n = \sum_{k=0}^n {n \choose k}x^{n-k}y^k.} This means you add up all the terms from to .

A simpler version of the formula is when $y$ is 1: 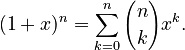Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle (1+x)^n = \sum_{k=0}^n {n \choose k}x^k.} This can also be written out as: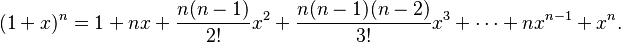 $(1+x)^n = 1 + n x + \frac{n(n-1)}{2!}x^2 + \frac{n(n-1)(n-2)}{3!}x^3 + \cdots + n x^{n-1} + x^n.$

Examples of Binomial Expansion

Let's look at some examples of the binomial theorem in action: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \begin{align} (x+y)^0 & = 1, \\[8pt] (x+y)^1 & = x + y, \\[8pt] (x+y)^2 & = x^2 + 2xy + y^2, \\[8pt] (x+y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3, \\[8pt] (x+y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4. \end{align}}

Notice these patterns in the expansion of $(x + y) n$ :

The power of $x$ starts at $n$ and goes down to 0.
The power of $y$ starts at 0 and goes up to $n$ .
The sum of the powers of $x$ and $y$ in each term is always $n$ .
The numbers in front of the terms (the coefficients) are from the $n$ th row of Pascal's triangle.
There are $n + 1$ terms in the final expanded form.

For example, with $(x+y) 3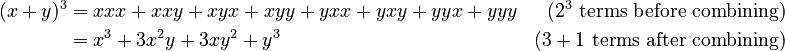$ : Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \begin{align} (x+y)^3 & = xxx + xxy + xyx + xyy + yxx + yxy + yyx + yyy & (2^3 \text{ terms before combining}) \\ & = x^3 + 3x^2y + 3xy^2 + y^3 & (3 + 1 \text{ terms after combining}) \end{align}} The coefficients (1, 3, 3, 1) add up to , which is $23$ .

Using Specific Numbers

Let's try an example where $y$ is a specific number, like 2: 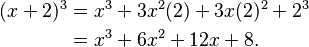${\displaystyle \begin{align} (x+2)^3 &= x^3 + 3x^2(2) + 3x(2)^2 + 2^3 \\ &= x^3 + 6x^2 + 12x + 8. \end{align}}$

What if $y$ is a negative number? Let's use -2: 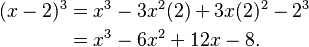${\displaystyle \begin{align} (x-2)^3 &= x^3 - 3x^2(2) + 3x(2)^2 - 2^3 \\ &= x^3 - 6x^2 + 12x - 8. \end{align}}$ Notice how the signs alternate!

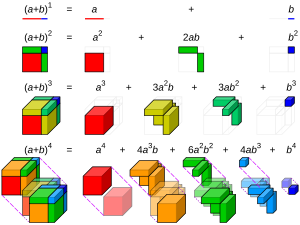
Visualizing the Theorem

Visualisation of binomial expansion up to the 4th power

You can see the binomial theorem in real life!

For n = 2, . Imagine a big square with sides of length a + b. You can cut this square into:
- A smaller square with side $a$ (area $a 2$ ).
- Another smaller square with side $b$ (area $b 2$ ).
- Two rectangles with sides $a$ and $b$ (area $ab$ each, so $2ab$ total).
For n = 3, . Imagine a big cube with sides of length a + b. You can cut this cube into:
- A smaller cube with side $a$ (volume $a 3$ ).
- Another smaller cube with side $b$ (volume $b 3$ ).
- Three rectangular boxes that are $a \times a \times b$ (volume $a 2 b$ each, so $3a 2 b$ total).
- Three rectangular boxes that are $a \times b \times b$ (volume $ab 2$ each, so $3ab 2$ total).

Understanding Binomial Coefficients

The numbers that appear in the binomial expansion are called binomial coefficients. We usually write them as 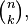$\tbinom{n}{k},$ and say " $n$ choose $k$ ."

How to Calculate Them

The coefficient of $x n - k y k$ is found using this formula: 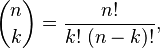$\binom{n}{k} = \frac{n!}{k! \; (n-k)!},$ The "!" symbol means factorial. For example, $5!$ means $5 \times 4 \times 3 \times 2 \times 1$ . Even though the formula looks like a fraction, the binomial coefficient 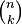$\tbinom{n}{k}$ will always be a whole number.

How the Binomial Theorem is Proved

There are different ways to prove the binomial theorem. Here are two common methods:

Proof by Counting (Combinatorial Proof)

Let's look at . When you multiply this out, you pick either an $x$ or a $y$ from each of the three brackets. For example, to get $xy 2$ , you need to pick one $x$ and two $y$ 's. The possible ways to do this are:

$xyy$ (pick $x$ from the 1st bracket, $y$ from the 2nd, $y$ from the 3rd)
$yxy$ (pick $y$ from the 1st, $x$ from the 2nd, $y$ from the 3rd)
$yyx$ (pick $y$ from the 1st, $y$ from the 2nd, $x$ from the 3rd)

There are 3 ways to get $xy 2$ , so its coefficient is 3. This is exactly what 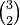Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tbinom{3}{2} (3 choose 2) equals!

In general, for $(x + y) n$ , the coefficient of $x n - k y k$ is the number of ways you can choose $k$ of the $y$ 's (and $n - k$ of the $x$ 's) from the $n$ brackets. This is exactly what the binomial coefficient 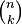$\tbinom{n}{k}$ represents.

Proof by Induction

Another way to prove the theorem is using mathematical induction. This is like a chain reaction proof: 1. Base Case: Show the theorem works for the smallest value, $n = 0$ . * . * The formula gives 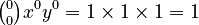Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tbinom{0}{0}x^0y^0 = 1 \times 1 \times 1 = 1 . So it works! 2. Inductive Step: Assume the theorem works for some whole number $n$ . Then show that it must also work for $n + 1$ . * We know . * Using our assumption for $(x+y) n$ , we can multiply it by $(x+y)$ . * When you do this, the coefficients for $(x+y) n+1$ come from adding two coefficients from the $n$ th row. This is exactly Pascal's identity: 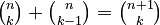Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tbinom{n}{k} + \tbinom{n}{k-1} = \tbinom{n+1}{k} . * Since the coefficients match Pascal's identity, the theorem holds for $n + 1$ . Because it works for $n = 0$ and if it works for $n$ it also works for $n + 1$ , it must work for all whole numbers $n$ !

Broader Uses of the Binomial Theorem

Newton's Generalization

Isaac Newton made the binomial theorem even more powerful. He showed it can work even when the exponent $n$ is not a whole number (it can be a real number or even a complex number). When $n$ is not a whole number, the expansion becomes an infinite series (a sum that goes on forever). For example, for the square root (which is power 1/2): 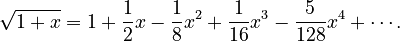Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \sqrt{1+x} = 1 + \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16}x^3 - \frac{5}{128}x^4 + \cdots.} This is super useful in calculus and other advanced math.

Multinomial Theorem

The binomial theorem is for expressions with two terms (like $x + y$ ). But what if you have more than two terms, like $(x 1 + x 2 + x 3) n$ ? The multinomial theorem helps with this! 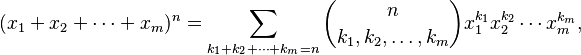$(x_1 + x_2 + \cdots + x_m)^n = \sum_{k_1+k_2+\cdots +k_m = n} \binom{n}{k_1, k_2, \ldots, k_m} x_1^{k_1} x_2^{k_2} \cdots x_m^{k_m},$ The coefficients 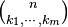$\tbinom{n}{k_1,\cdots,k_m}$ are called multinomial coefficients. They are calculated as: 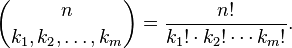$\binom{n}{k_1, k_2, \ldots, k_m} = \frac{n!}{k_1! \cdot k_2! \cdots k_m!}.$ These coefficients tell you how many ways you can divide a set of $n$ items into smaller groups of sizes $k 1, k 2, ..., k m$ .

General Leibniz Rule

The binomial theorem also has a "cousin" in calculus called the General Leibniz rule. It helps find the $n$ th derivative of a product of two functions. It looks very similar to the binomial theorem: 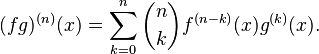$(fg)^{(n)}(x) = \sum_{k=0}^n \binom{n}{k} f^{(n-k)}(x) g^{(k)}(x).$ Here, $(n)$ means the $n$ th derivative.

Real-World Applications

Trigonometry Identities

The binomial theorem can be used with complex numbers and de Moivre's formula to find cool rules for sine and cosine functions. For example, to find formulas for $cos(2x)$ and $sin(2x)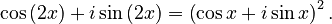$ : Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \cos\left(2x\right)+i\sin\left(2x\right) = \left(\cos x+i\sin x\right)^2.} Expanding the right side using the binomial theorem gives: 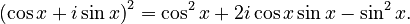Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \left(\cos x + i\sin x\right)^2 = \cos^2 x + 2i \cos x \sin x - \sin^2 x.} By comparing the real and imaginary parts, we get: 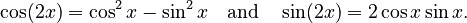Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \cos(2x) = \cos^2 x - \sin^2 x \quad\text{and}\quad\sin(2x) = 2 \cos x \sin x.} These are the well-known double-angle identities!

Understanding the Number e

The special mathematical constant $e$ (about 2.718) is often defined using a limit: 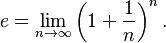$e = \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^n.$ If you apply the binomial theorem to the expression inside the limit, you can see how $e$ is related to an infinite series: 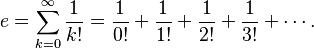$e=\sum_{k=0}^\infty\frac{1}{k!}=\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots.$ This shows how the binomial theorem helps us understand fundamental numbers in mathematics.

Probability

The binomial theorem is also used in probability. For example, it helps understand the binomial distribution, which describes the probability of getting a certain number of successes in a series of independent trials (like flipping a coin multiple times).

In Abstract Algebra

The binomial theorem isn't just for numbers! It also works for elements $x$ and $y$ in a ring (a type of mathematical structure), as long as $xy = yx$ (meaning the order of multiplication doesn't matter). This is useful when working with things like matrices, especially when calculating powers of matrices that "commute" (multiply in any order).