Pascal's triangle facts for kids

This picture shows the first eight rows of Pascal's triangle.

Pascal's triangle is a cool pattern of numbers shaped like a triangle. It's used in many areas of mathematics, like figuring out chances (probability) or counting different ways things can be arranged (combinatorics).

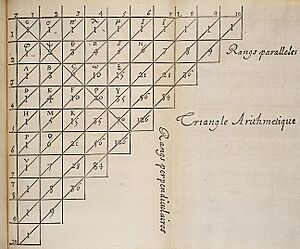
Even though it's named after the French mathematician Blaise Pascal, people in places like Persia, India, and China knew about this triangle centuries before him!

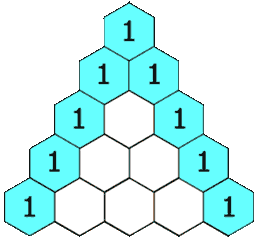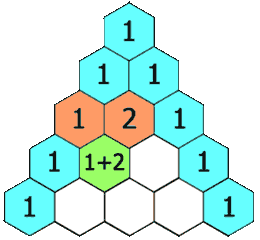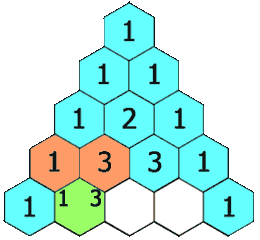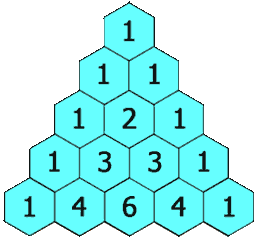
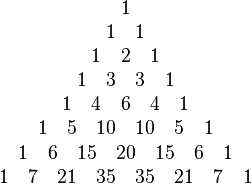
The rows of the triangle usually start counting from row 0 at the very top. Each number in a row is found by adding the two numbers directly above it. If there's no number above (like at the edges), you just pretend there's a zero there.

For example, to get the '2' in row 2, you add the '1' and '1' from row 1. To get the '4' in row 4, you add the '1' and '3' from row 3, or the '3' and '1' from row 3. The edges of the triangle are always '1's.

How to Build Pascal's Triangle

In Pascal's triangle, each number is the sum of the two numbers directly above it.

Building Pascal's triangle is like following a simple rule:

• Start with a '1' at the very top (this is row 0).
• For every new row, begin and end with a '1'.
• To find any other number in a row, just add the two numbers directly above it from the row before.
• If there's only one number above, or no number, treat the missing spot as a '0'.

This simple rule helps create all the numbers in the triangle.

A Quick Look at History

Yang Hui's triangle, shown with Chinese rod numerals, from a book in 1303.

Blaise Pascal's drawing of the triangle.

The amazing number pattern in Pascal's triangle was known long before Blaise Pascal.

• In Persia, a mathematician named Al-Karaji (who lived from 953 to 1029) wrote about it. Later, another Persian mathematician, Omar Khayyám (1048–1131), also studied it. That's why it's sometimes called Khayyam's triangle in Iran.
• In China, the triangle was known in the 11th century thanks to Jia Xian (1010–1070). In the 13th century, Yang Hui (1238–1298) showed the triangle, and it's still called Yang Hui's triangle in China.
• In Europe, it first appeared in a book by Jordanus de Nemore in the 13th century.
• In Italy, it's known as Tartaglia's triangle, named after Niccolò Fontana Tartaglia (1500–1577), who published parts of it in 1556.

Blaise Pascal wrote a book about the triangle in 1665. In it, he gathered many known facts about the triangle. He also used it to solve problems in probability theory, which is about how likely events are to happen. Later, other mathematicians named the triangle after him.

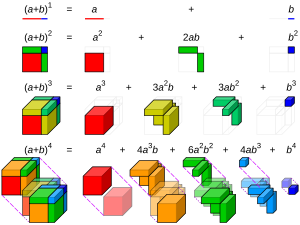
Binomial Expansions

Visualizing how binomial expansions work up to the 4th power.

Pascal's triangle helps us quickly find the numbers (called coefficients) when you multiply out expressions like (x + y) raised to a power. This is called a binomial expansion.

Let's look at an example:

• (x + y)⁰ = 1 (This matches row 0: 1)
• (x + y)¹ = 1x + 1y (This matches row 1: 1, 1)
• (x + y)² = 1x² + 2xy + 1y² (This matches row 2: 1, 2, 1)
• (x + y)³ = 1x³ + 3x²y + 3xy² + 1y³ (This matches row 3: 1, 3, 3, 1)

See the pattern? The numbers in each row of Pascal's triangle are exactly the coefficients you need for these expansions! This is a super useful rule called the binomial theorem.

Six rows of Pascal's triangle shown as binomial coefficients.

Another cool thing: if you add up all the numbers in any row of Pascal's triangle, the sum will be a power of 2.

• Row 0: 1 = 2⁰
• Row 1: 1 + 1 = 2 = 2¹
• Row 2: 1 + 2 + 1 = 4 = 2²
• Row 3: 1 + 3 + 3 + 1 = 8 = 2³

And so on! The sum of numbers in row 'n' is always 2ⁿ.

Combinations

Pascal's triangle is also great for figuring out combinations. A combination is a way of choosing items from a group where the order doesn't matter. For example, if you have 10 friends and need to pick 3 for a team, how many different teams can you make?

The number of ways to choose 'k' items from a group of 'n' items is written as (read as "n choose k"). This is exactly what each number in Pascal's triangle represents!

To find the answer, you just look at row 'n' and then count 'k' spots over (starting from 0).

• For example, if you have 10 candidates for 8 jobs, you want to know "10 choose 8".
• Go to row 10 of Pascal's triangle.
• Count 8 spots over (0, 1, 2, 3, 4, 5, 6, 7, 8).
• The number you find there is 45. So, there are 45 ways to pick 8 people from 10.

Cool Patterns and Properties

Pascal's triangle is full of hidden patterns!

Each frame shows a row in Pascal's triangle. Light pixels are ones, dark pixels are zeroes in binary.

The numbers of ways to break down 'n'+1 into 'k'+1 ordered parts form Pascal's triangle.

Rows

• Sum of Rows: As we saw, the sum of numbers in row 'n' is 2ⁿ.
• Prime Number Rows: If a row number 'p' is a prime number (like 5, 7, 11), then all the numbers in that row (except for the 1s at the ends) can be divided by 'p' evenly. For example, in row 5 (1, 5, 10, 10, 5, 1), the numbers 5 and 10 are all multiples of 5.
• Odd Numbers: If you color all the odd numbers in Pascal's triangle, you'll see a pattern that looks like a famous fractal called the Sierpinski triangle.
• Alternating Sums: If you add and subtract the numbers in a row, the answer is always 0. For example, row 6 is 1, 6, 15, 20, 15, 6, 1. So, 1 - 6 + 15 - 20 + 15 - 6 + 1 = 0.

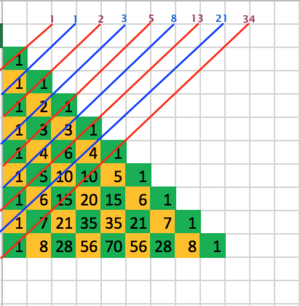
Diagonals

How to get simplex numbers from a left-justified Pascal's triangle.

The diagonals of Pascal's triangle also have special number patterns:

• The first two diagonals (the ones on the very edges) are just all '1's.
• The next two diagonals (moving inwards) are the natural numbers: 1, 2, 3, 4, ...
• The next pair of diagonals are the triangular numbers: 1, 3, 6, 10, 15, ... (These are numbers you get by adding 1, then 1+2, then 1+2+3, and so on).
• The next pair are the tetrahedral numbers: 1, 4, 10, 20, ... (These are like 3D triangular numbers).

Overall Patterns

			10
		10	20

Pascal's triangle on a grid shows how many different shortest paths there are to each square, moving only right or down.

• Grid Paths: Imagine a grid. The numbers in Pascal's triangle tell you how many different shortest paths you can take from the top corner to any other spot in the triangle, only moving down or right. This is like how a Plinko game works!

Image:Pascal's Triangle 4 paths.svg

• Fibonacci Numbers: If you add up the numbers along the diagonals that go from top-right to bottom-left (if the triangle is left-justified), you'll find the Fibonacci numbers!

1
1	1
1	2	1
1	3	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1
1	7	21	35	35	21	7	1

The Fibonacci sequence found in Pascal's triangle.

Pascal's Triangle in Higher Dimensions

Pascal's triangle can be extended into 3D and even higher dimensions!

• The 3D version is called Pascal's pyramid or Pascal's tetrahedron.
• The general versions for even more dimensions are known as Pascal's simplices. These still follow similar rules of adding numbers to build the next layer.

Images for kids

• 

  A level-4 approximation to a Sierpinski triangle obtained by shading the first 32 rows of a Pascal triangle white if the binomial coefficient is even and black if it is odd.