Niccolò Fontana Tartaglia facts for kids
Quick facts for kids
Niccolò Fontana Tartaglia
|
|
|---|---|
_Portretten_van_beroemde_Europese_geleerden_(serietitel)_Virorum_doctorum_de_Disciplinis_benemerentium_effigies_(serietitel),_RP-P-1909-4459.jpg) |
|
| Born |
Niccolò Fontana
1499/1500 |
| Died | 13 December 1557 |
| Nationality | Italian |
| Known for | Cardano–Tartaglia formula Early research into ballistics Tartaglia's triangle |
| Scientific career | |
| Fields | Mathematics, engineering |
| Notable students | Ostilio Ricci |
Niccolò Fontana Tartaglia (1499/1500 – 13 December 1557) was a famous Italian mathematician and engineer. He was also a surveyor and a bookkeeper. He lived in the Republic of Venice.
Tartaglia published many important books. These included the first Italian translations of ancient Greek mathematicians like Archimedes and Euclid. He also wrote a highly praised collection of mathematical works.
He was the first person to use mathematics to study how cannonballs fly. This field is called ballistics. He wrote about it in his book Nova Scientia (A New Science) in 1537. Later, Galileo built on Tartaglia's ideas. Tartaglia also wrote a guide on how to rescue sunken ships.
Contents
About Niccolò Tartaglia's Life
Niccolò Fontana was born in Brescia. His father, Michele Fontana, delivered mail between towns. In 1506, robbers killed Michele, leaving Niccolò, his two siblings, and his mother very poor.
More trouble came in 1512 during a war. French soldiers attacked Brescia. Niccolò and his family hid in a church. A French soldier found them and wounded Niccolò's face with a sword. His mother helped him recover, but the injury left him with a speech problem. This led to his nickname "Tartaglia," which means "stammerer." Because of his scars, he never shaved and grew a beard.
Around 1517, Tartaglia moved to Verona. Then, in 1534, he moved to Venice. Venice was a big trading city and a center for new ideas during the Italian Renaissance. It was also a major printing hub. This meant even poor scholars like Tartaglia could find old books. For example, he found a Latin book by Archimedes in 1531 from a sausage seller in Verona!
He died in Venice.
Tartaglia's Work on Ballistics
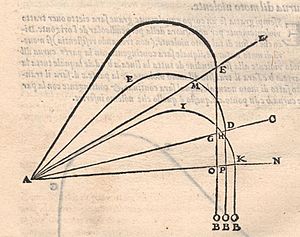
Nova Scientia (A New Science), published in 1537, was Tartaglia's first book. In this book, he used mathematical ideas to explain how objects move. Before him, people often used older ideas from Aristotle to describe motion. Tartaglia showed that math could better explain how things like cannonballs fly.
One of his key discoveries was about cannons. He found that a cannonball would travel the farthest if the cannon was aimed at a 45-degree angle to the ground.
Tartaglia thought a cannonball's flight had three parts. First, it flew in a straight line from the cannon. Then, it started to curve downwards in a circular path. Finally, it dropped straight down to the ground. He used math to figure out the length of that first straight path.
Tartaglia's work on military science became very popular across Europe. Gunners used his ideas for centuries. Even Galileo, another famous scientist, studied Tartaglia's books on ballistics.
Important Translations by Tartaglia
Tartaglia helped spread the ideas of ancient Greek mathematicians. He believed that math was key to understanding how the world works.
In 1543, he published a Latin version of some of Archimedes' works. This book included Archimedes' writings on parabolas, circles, centers of gravity, and floating objects. Some of these works had never been published before. Tartaglia later translated some of Archimedes' texts into Italian. These translations were widely read and likely helped Galileo learn about Archimedes.
Tartaglia's Italian translation of Euclid's Elements in 1543 was very important. It was the first time Euclid's famous geometry book was translated into any modern European language. For 200 years, Euclid had been taught using Latin versions that had mistakes. Tartaglia's edition was based on a correct Greek text. This meant that a difficult part of Euclid's book, about proportions, finally made sense.
His Euclid translation was reprinted many times. It helped many people in Italy, who were not university scholars, learn more about mathematics. This knowledge was very useful for scientists like Galileo and Archimedes.
General Treatise on Number and Measure
Tartaglia was a master of practical mathematics. He came from a tradition of "abaco schools" in Italy. These schools taught math useful for merchants and traders. Teachers like Tartaglia taught using paper and pen, showing students how to solve problems step-by-step.
Tartaglia's greatest work was the General Trattato di Numeri et Misure (General Treatise on Number and Measure). This huge book was 1500 pages long and had six parts. He wrote it in the Venetian language. The first three parts came out around the time he died in 1556. The last three parts were published after his death in 1560.
Part I of the book was about business math. It covered topics like working with different types of money, exchanging currencies, calculating interest, and sharing profits in companies. The book had many examples and clear rules for solving problems.
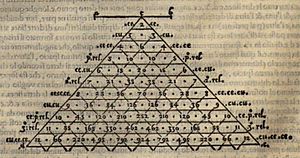
Part II dealt with more general math problems. These included number patterns, powers, and how to work with roots. It also included what we now call Tartaglia's triangle.
Part IV focused on shapes like triangles, regular polygons, and 3D shapes. It also covered Archimedes' ideas about circles and spheres.
Tartaglia's Triangle
Tartaglia was very good at working with binomial expansions. These are ways to multiply expressions like (a+b) raised to a power. He included many examples in his General Trattato.
He knew about Pascal's triangle a hundred years before Pascal. This triangle helps find the numbers needed for binomial expansions. Tartaglia showed how to build the triangle by adding numbers from the row above. For example, 15 and 20 in one row add up to 35 in the row below.
Solving Cubic Equations
Tartaglia is also famous for his arguments with another mathematician, Gerolamo Cardano. In 1539, Cardano convinced Tartaglia to share his secret method for solving cubic equations. These are equations where the highest power of the unknown number is three (like x³). Tartaglia shared his solutions in a poem, after Cardano promised not to publish them.
Later, Cardano saw some unpublished work by Scipione del Ferro. Del Ferro had found the same solution as Tartaglia independently. Since del Ferro's work was older, Cardano felt he could break his promise. He included Tartaglia's solution in his next book.
Even though Cardano gave Tartaglia credit, Tartaglia was very angry. This led to a public math challenge between Tartaglia and Cardano's student, Ludovico Ferrari. Today, mathematical historians give credit to both Cardano and Tartaglia for the formula to solve cubic equations. It is called the "Cardano–Tartaglia formula".
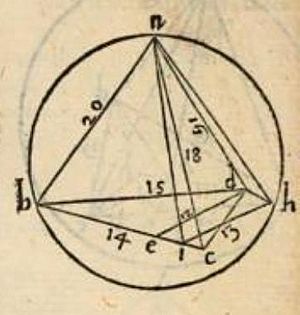
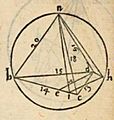
Calculating the Volume of a Tetrahedron
Tartaglia was excellent at calculations and understanding 3D shapes. In Part IV of his General Trattato, he showed how to find the height of a pyramid with a triangular base. This shape is also called an irregular tetrahedron.
He used a specific example with a base triangle and edges of certain lengths. He showed how to break down the problem into smaller steps. He used a formula to find the height of a triangle based on its sides. This formula comes from the Law of Cosines.
Tartaglia's method was correct, even though he made a small mistake in one number. He always used fractions, as decimal fractions were invented later. His way of solving the problem was very modern, showing a step-by-step method for finding the height of many different irregular tetrahedrons.
Images for kids
-
Portrait of Niccolò Fontana Tartaglia.
-
Various projectile trajectories from Nova Scientia.
-
General trattato di numeri et misure, 1556.
-
Tartaglia's triangle from General Trattato di Numeri et Misure, Part II, Book 2, p. 69.
-
13-14-15-20-18-16 pyramid from the General Trattato di Numeri et Misure, Part IV, Book 2, p. 35.
See also
In Spanish: Niccolò Fontana Tartaglia para niños
