Binomial expansion facts for kids

Kids Encyclopedia Facts

Binomial expansion is a cool way to multiply out special math problems. It helps you expand expressions that look like 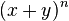$(x+y)^n$ . Think of it like taking a shortcut instead of multiplying everything by hand many times! There are a few main ways to do this.

Basic Formulas for Binomials
Using Pascal's Triangle for Expansion
- More Examples
See also

Basic Formulas for Binomials

There are three simple binomial expansion formulas that are good to know. These are for when the power n is 2.

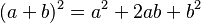$(a+b)^2 = a^2 + 2 ab + b^2$		1st (Adding)
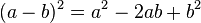$(a-b)^2 = a^2 - 2 ab + b^2$		2nd (Subtracting)
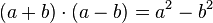$(a+b) \cdot (a-b) = a^2 - b^2$		3rd (Adding and Subtracting)

These formulas come from simply multiplying the terms. Let's look at how they work:

For 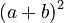Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a+b)^2 , it means 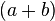Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a+b) multiplied by Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a+b) .

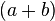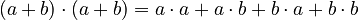* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a+b) \cdot (a+b) = a \cdot a + a \cdot b + b \cdot a + b \cdot b * This simplifies to 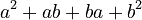Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^2 + ab + ba + b^2 . * Since 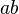$ab$ and Failed to parse (Missing <code>texvc</code> executable. 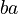Please see math/README to configure.): ba are the same, we get Failed to parse (Missing <code>texvc</code> executable. 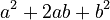Please see math/README to configure.): a^2 + 2ab + b^2 .

For 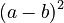Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a-b)^2 , it means 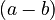Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a-b) multiplied by Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a-b) .

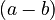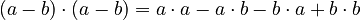* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a-b) \cdot (a-b) = a \cdot a - a \cdot b - b \cdot a + b \cdot b * This simplifies to 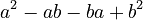Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^2 - ab - ba + b^2 . * Again, 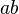$ab$ and Failed to parse (Missing <code>texvc</code> executable. 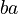Please see math/README to configure.): ba are the same, so we get Failed to parse (Missing <code>texvc</code> executable. 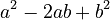Please see math/README to configure.): a^2 - 2ab + b^2 .

For 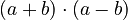Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a+b) \cdot (a-b) , it's a bit different.

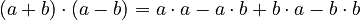* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (a+b) \cdot (a-b) = a \cdot a - a \cdot b + b \cdot a - b \cdot b * This simplifies to 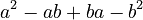Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^2 - ab + ba - b^2 . * The 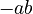Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): -ab and Failed to parse (Missing <code>texvc</code> executable. 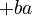Please see math/README to configure.): +ba cancel each other out! * So, you are left with just Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): a^2 - b^2 .

Using Pascal's Triangle for Expansion

When the power n in 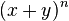$(x+y)^n$ is a whole number (like 0, 1, 2, 3, and so on), we can use a special pattern called Pascal's Triangle.

Pascal's Triangle is a number pattern where each number is the sum of the two numbers directly above it. It looks like this:

Row 0: 1
Row 1: 1 1
Row 2: 1 2 1
Row 3: 1 3 3 1
Row 4: 1 4 6 4 1
And so on!

To expand an expression like 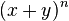$(x+y)^n$ using Pascal's Triangle:

Find the row in Pascal's Triangle that matches your power n. For example, if you have 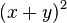$(x+y)^2$ , you use Row 2 (1, 2, 1).
For the first term ( 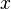$x$ ), its power starts at n and goes down by 1 each time.
For the second term ( 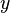$y$ ), its power starts at 0 and goes up by 1 each time, until it reaches n.
Multiply the numbers from Pascal's Triangle with the terms you've created.

Let's try an example: expanding 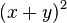$(x+y)^2$ .

Row 2 of Pascal's Triangle is (1, 2, 1).
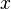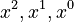The powers of $x$ will be Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^2, x^1, x^0 .
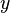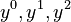The powers of $y$ will be Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): y^0, y^1, y^2 .
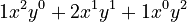Combine them: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1x^2y^0 + 2x^1y^1 + 1x^0y^2 .
Remember that anything to the power of 0 is 1. So 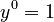Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): y^0=1 and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^0=1 .
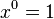This simplifies to 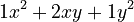Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1x^2 + 2xy + 1y^2 , or just 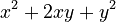Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x^2 + 2xy + y^2 . This matches our first basic formula!

Here's another example: 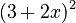Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (3+2x)^2 .

Use Row 2 of Pascal's Triangle: (1, 2, 1).
The first term is 3, the second term is $2x$ .
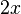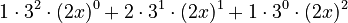
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 3^2 \cdot (2x)^0 + 2 \cdot 3^1 \cdot (2x)^1 + 1 \cdot 3^0 \cdot (2x)^2
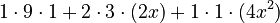
Calculate the powers: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 9 \cdot 1 + 2 \cdot 3 \cdot (2x) + 1 \cdot 1 \cdot (4x^2)
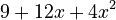Multiply everything: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 9 + 12x + 4x^2 .

So, as a general rule for 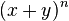$(x+y)^n$ : You add up terms where each term has:

A number from Pascal's Triangle (let's call it $a_i$ ).
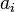The first term ( 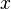$x$ ) raised to a power that goes down from n to 0.
The second term ( 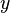$y$ ) raised to a power that goes up from 0 to n.

More Examples

Let's look at a few more examples to see how this works with higher powers.

Expanding (5+3x)³

Here, n is 3. So we use Row 3 of Pascal's Triangle: (1, 3, 3, 1).

The first term is 5.
The second term is $3x$ .
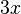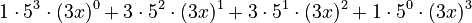
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 5^3 \cdot (3x)^0 + 3 \cdot 5^2 \cdot (3x)^1 + 3 \cdot 5^1 \cdot (3x)^2 + 1 \cdot 5^0 \cdot (3x)^3
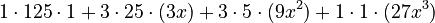
Calculate the powers: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 125 \cdot 1 + 3 \cdot 25 \cdot (3x) + 3 \cdot 5 \cdot (9x^2) + 1 \cdot 1 \cdot (27x^3)
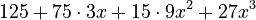
Multiply: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 125 + 75 \cdot 3x + 15 \cdot 9x^2 + 27x^3
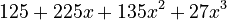
Final answer: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 125 + 225x + 135x^2 + 27x^3

Expanding (5-3x)³

This is similar, but the second term is 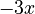Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): -3x .

Use Row 3 of Pascal's Triangle: (1, 3, 3, 1).
The first term is 5.
The second term is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): -3x .
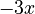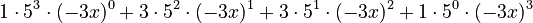
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 5^3 \cdot (-3x)^0 + 3 \cdot 5^2 \cdot (-3x)^1 + 3 \cdot 5^1 \cdot (-3x)^2 + 1 \cdot 5^0 \cdot (-3x)^3
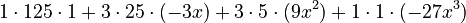
Calculate the powers (be careful with negative signs!): Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 125 \cdot 1 + 3 \cdot 25 \cdot (-3x) + 3 \cdot 5 \cdot (9x^2) + 1 \cdot 1 \cdot (-27x^3)
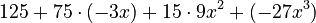
Multiply: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 125 + 75 \cdot (-3x) + 15 \cdot 9x^2 + (-27x^3)
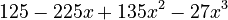
Final answer: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 125 - 225x + 135x^2 - 27x^3

Expanding (7+4x²)⁵

Here, n is 5. So we use Row 5 of Pascal's Triangle: (1, 5, 10, 10, 5, 1).

The first term is 7.
The second term is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 4x^2 .
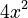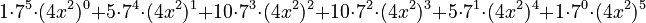
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 7^5 \cdot (4x^2)^0 + 5 \cdot 7^4 \cdot (4x^2)^1 + 10 \cdot 7^3 \cdot (4x^2)^2 + 10 \cdot 7^2 \cdot (4x^2)^3 + 5 \cdot 7^1 \cdot (4x^2)^4 + 1 \cdot 7^0 \cdot (4x^2)^5
Calculate the powers:

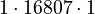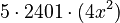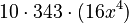* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 1 \cdot 16807 \cdot 1 * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 5 \cdot 2401 \cdot (4x^2) * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 10 \cdot 343 \cdot (16x^4) * Failed to parse (Missing <code>texvc</code> executable. 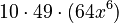Please see math/README to configure.): 10 \cdot 49 \cdot (64x^6) * Failed to parse (Missing <code>texvc</code> executable. 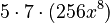Please see math/README to configure.): 5 \cdot 7 \cdot (256x^8) * Failed to parse (Missing <code>texvc</code> executable. 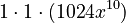Please see math/README to configure.): 1 \cdot 1 \cdot (1024x^{10})

Multiply each part:

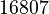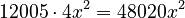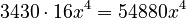* Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 16807 * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 12005 \cdot 4x^2 = 48020x^2 * Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 3430 \cdot 16x^4 = 54880x^4 * Failed to parse (Missing <code>texvc</code> executable. 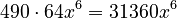Please see math/README to configure.): 490 \cdot 64x^6 = 31360x^6 * Failed to parse (Missing <code>texvc</code> executable. 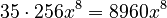Please see math/README to configure.): 35 \cdot 256x^8 = 8960x^8 * Failed to parse (Missing <code>texvc</code> executable. 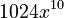Please see math/README to configure.): 1024x^{10}

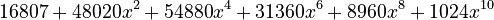
Final answer: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 16807 + 48020x^2 + 54880x^4 + 31360x^6 + 8960x^8 + 1024x^{10}