Pascal's Triangle facts for kids
Pascal's Triangle is a special kind of number pattern shaped like a triangle. It's named after a French mathematician named Blaise Pascal. But guess what? People in China were using this triangle about 300 years before Pascal! It's a really cool tool that helps us understand different things in math, like how likely events are to happen (probability) and how to expand certain math problems.
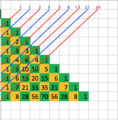
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1
Contents
How to Build Pascal's Triangle
Building Pascal's Triangle is quite simple and fun!
- Start with the number 1 at the very top. This is your first row.
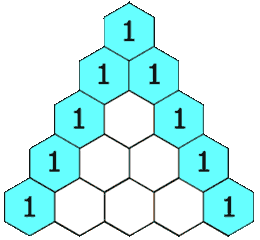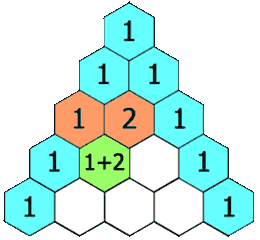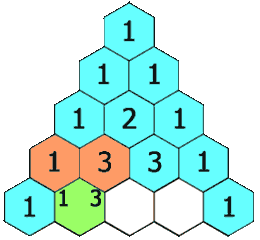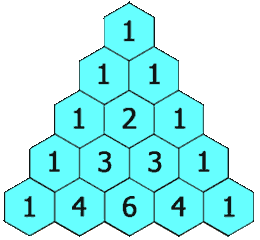
- For the next rows, you get each new number by adding the two numbers directly above it.
- If there's only one number above (like at the edges), imagine there's a zero next to it. So, 1 + 0 equals 1. This means the numbers on the outside edges of the triangle are always 1.
Let's look at an example: In the fourth row, you see the numbers 1 and 3. If you add them together (1 + 3), you get 4. This 4 is one of the numbers in the fifth row, right below where the 1 and 3 were.
History of Pascal's Triangle
Even though it's called Pascal's Triangle, it was known and used in different parts of the world long before Blaise Pascal was born.
- In China, mathematicians like Yang Hui used it in the 13th century. They called it "Yang Hui's Triangle." It was used to solve problems in algebra.
- Ancient Indian mathematicians also knew about this pattern, using it for things like poetry and counting combinations.
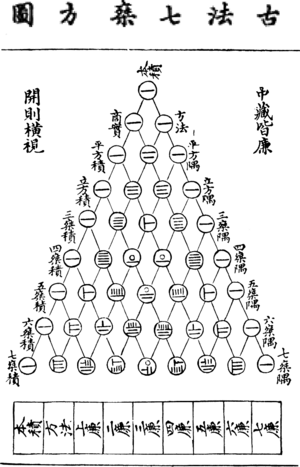
What Pascal's Triangle is Used For
Pascal's Triangle is super useful in many areas of math.
Probability and Combinations
One big use is in probability, which is about how likely something is to happen. It also helps with combinations, which is about how many different ways you can choose things from a group.
For example, if you flip a coin three times, how many ways can you get two heads and one tail? The numbers in Pascal's Triangle can help you figure this out quickly!
Binomial Expansion
Pascal's Triangle is also used in something called "binomial expansion." A binomial is a math expression with two terms, like (x + y). When you raise a binomial to a power, like (x + y)2 or (x + y)3, the numbers in Pascal's Triangle tell you the coefficients (the numbers in front of the variables) in the answer.
For example:
- (x + 1)2 = 1x2 + 2x + 12
Notice the numbers 1, 2, and 1. These are exactly the numbers in the third row of Pascal's Triangle (if you count the top '1' as row zero).
Cool Properties of Pascal's Triangle
This triangle has many interesting features:
- Always Starts and Ends with 1: The first and last number in every row is always 1.
- Second Number is the Row Number: The second number in each row (from the left or right) is the same as the row number. For example, in row 4 (1, 4, 6, 4, 1), the second number is 4.
- Symmetrical Rows: Each row reads the same forwards and backwards. It's like a mirror! For example, row 4 is 1, 4, 6, 4, 1.
- Sum of Numbers in Each Row: If you add up all the numbers in a row, the sum is always a power of 2.
- The top row (just 1) sums to 1 (which is 20).
- The next row (1, 1) sums to 2 (which is 21).
- The row (1, 2, 1) sums to 4 (which is 22).
- The row (1, 3, 3, 1) sums to 8 (which is 23).
This pattern continues for all rows!
More Complex Versions
Pascal's Triangle can even be extended into higher dimensions!
- A 3D version is called a Pascal's pyramid or Pascal's tetrahedron.
- Even higher-dimensional versions are sometimes called "Pascal's simplex."
These are like the triangle, but they involve adding numbers in three or more directions to build a pyramid or other shapes.
Images for kids
-
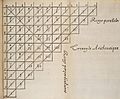
Meru Prastaara (मेरु प्रस्तार) as used in Indian manuscripts, derived from Pingala's formulae. Manuscript from Raghunath Library J&K; 755 AD
-
Pascal's version of the triangle
-
Fibonacci sequence in Pascal's triangle
See also
 In Spanish: Triángulo de Pascal para niños
In Spanish: Triángulo de Pascal para niños