De Moivre's formula facts for kids
De Moivre's formula is a special rule in mathematics that helps us work with complex numbers and trigonometry. It was named after a mathematician named Abraham de Moivre. This formula is super useful because it connects these two important areas of math.
The main idea of de Moivre's formula is that if you have a complex number written in a special way (using angles), you can easily raise it to any power. It states that for any real number x (which represents an angle) and any whole number n, the following is true:
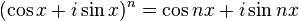
Here, `cos` stands for cosine and `sin` stands for sine, which are functions from trigonometry that relate to angles. The letter `i` is the imaginary unit, which is a special number where `i` squared equals `-1`.
Contents
What are Complex Numbers?
To understand de Moivre's formula, you first need to know about complex numbers. A complex number is a number that has two parts: a "real" part and an "imaginary" part. It's usually written as `a + bi`, where `a` and `b` are regular numbers, and `i` is the imaginary unit.
For example, `3 + 2i` is a complex number. The `3` is the real part, and `2i` is the imaginary part. These numbers are very useful in many areas, like physics and engineering.
How Does it Connect to Angles?
Complex numbers can also be thought of as points on a special graph. When you connect these points to the center of the graph, you get a line. The length of this line and the angle it makes with the horizontal axis can describe the complex number. This is called the "polar form."
In polar form, a complex number `z` can be written as `r(cos θ + i sin θ)`.
- `r` is the length of the line (called the "modulus").
- `θ` (theta) is the angle the line makes with the horizontal axis.
This is where trigonometry comes in! Cosine and sine are functions that help us describe points on a circle using angles.
Using De Moivre's Formula
De Moivre's formula makes it easy to raise a complex number in polar form to a power. If you have a complex number `z` in polar form `r(cos θ + i sin θ)`, and you want to find `z` raised to the power of `n` (like `z` squared or `z` cubed), the formula tells you:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): z^n = [r(\cos \theta + i \sin \theta)]^n = r^n (\cos n \theta + i \sin n \theta)
This means you just raise the length `r` to the power of `n`, and you multiply the angle `θ` by `n`. It's much simpler than multiplying the complex number by itself `n` times!
Why is This Formula Important?
De Moivre's formula is very important because it helps solve many problems in math and science. For example, it can be used to find the "roots" of complex numbers. This means finding numbers that, when raised to a certain power, give you a specific complex number.
The formula can be proven using a method called mathematical induction, which is like building a proof step by step. It can also be proven using another famous math rule called Euler's formula, which also connects complex numbers, angles, and a special number `e` (Euler's number).
Related pages
