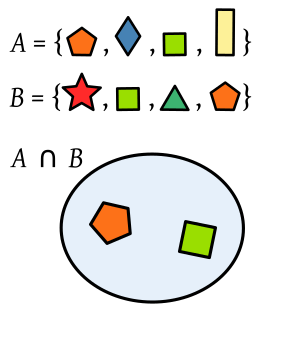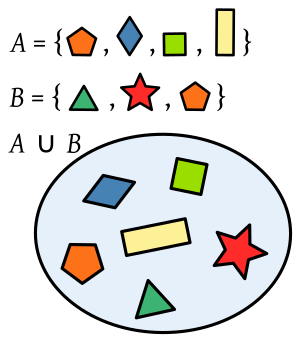Set facts for kids

A set is a group of things in mathematics. These things are called members or elements. A set is special because it's defined only by what's inside it. If two sets have the exact same members, they are considered the same set.
A set cannot have the same member more than once. The order of the members does not matter. Anything can be a member of a set. This even includes other sets!
Contents
What Can You Do with Sets?
Imagine a set is like a bag. You can put different things into this bag.
Checking for Members: "Element Of"
You might want to know if a certain thing is inside your set (or bag). Mathematicians call this "element of." If something is in the set, it is an element of that set.
The symbol for "element of" is 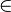 . So,
. So,  means that
means that 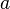 is in the set
is in the set 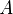 .
.
Unlike a real bag, a set only cares if an item is there or not. It doesn't matter if you have one orange or ten oranges. If an orange is in the set, it's just "an orange."
The Empty Set: An Empty Bag
Just like a bag can be empty, a set can also be empty. The empty set has nothing in it. It is also called the null set. The symbol for the empty set is 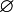 or
or 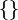 .
.
The Universe: All Things to Consider
Sometimes, when we talk about sets, we need to think about a bigger group that contains all the possible things we are interested in. This bigger group is called the universe.
For example, if you are looking at sets of different types of American cars, the universe would be the set of all American cars. The universe is usually shown with the letter 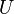 .
.
Comparing Sets: Are They the Same?
You can compare two sets to see if they are equal. This is like looking into two different bags. If they contain the exact same things, they are equal. The order of the items does not matter.
For example: If set 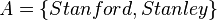 and set
and set 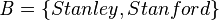 , these two sets are the same.
, these two sets are the same.
How Big Is a Set? Cardinality
Mathematicians often want to know how many elements are in a set. This is called the cardinality of the set. For sets with a limited number of items (called finite sets), the cardinality is simply a number.
- The empty set has a cardinality of 0.
- The set
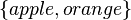 has a cardinality of 2.
has a cardinality of 2.
Two sets have the same cardinality if you can match up their elements perfectly. This means you can pair each element from one set with an element from the other set, with no elements left over.
For example: The set 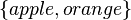 and the set
and the set  have the same cardinality. You could pair "apple" with "sun" and "orange" with "moon."
have the same cardinality. You could pair "apple" with "sun" and "orange" with "moon."
Infinite Cardinality: Sets That Never End
Sometimes, a set has an infinite number of elements. This means its cardinality is not a simple number. The set of all integers (whole numbers) is an example of a set with infinite cardinality.
Some infinite sets are "bigger" than others. For instance, there are more real numbers than there are natural numbers. This means you cannot perfectly pair up all natural numbers with all real numbers, even if you tried forever.
Countable and Uncountable Sets
If you can count the elements of a set, even if it takes forever, it's called a countable set. All finite sets are countable. Some infinite sets are also countable, like the natural numbers (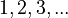 ). We call natural numbers "counting numbers" because we use them to count.
). We call natural numbers "counting numbers" because we use them to count.
An uncountable set is an infinite set that is impossible to count. No matter how you try to count its elements, you will always miss some. The set of all real numbers is an uncountable set. Even a small range of numbers, like from 0 to 1, can be uncountable!
Subsets: Sets Inside Other Sets
Look at set 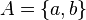 and set
and set 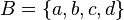 . You can see that every element in set
. You can see that every element in set  is also in set
is also in set 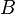 . When this happens, we say that
. When this happens, we say that  is a subset of
is a subset of 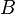 . It is written like this:
. It is written like this: 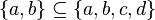 .
.
In general, if all elements of set  are also elements of set
are also elements of set 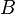 , we write:
, we write: 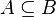 . This is usually read as "
. This is usually read as " is contained in
is contained in 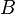 ."
."
Example: Every Chevrolet is an American car. So, the set of all Chevrolets is a subset of the set of all American cars.
How to Combine Sets: Set Operations
There are different ways to combine sets to create new ones.
Intersections: What Sets Have in Common
The intersection of two sets,  and
and 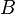 , is a new set. It contains all the elements that are in set
, is a new set. It contains all the elements that are in set  and also in set
and also in set 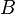 at the same time. The symbol for intersection is
at the same time. The symbol for intersection is  , so we write
, so we write 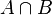 .
.
Example: If  is the set of all cheap cars, and
is the set of all cheap cars, and 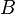 is the set of all American cars, then
is the set of all American cars, then 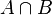 is the set of all cheap American cars.
is the set of all cheap American cars.
Unions: All Elements Together
The union of two sets,  and
and 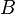 , is a new set. It contains all the elements that are in set
, is a new set. It contains all the elements that are in set  or in set
or in set 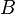 . This "or" includes elements that are in both sets. The symbol for union is
. This "or" includes elements that are in both sets. The symbol for union is  , so we write
, so we write  .
.
It's interesting to note that the intersection is always a subset of the union: 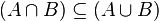 .
.
Example: If  is the set of all cheap cars, and
is the set of all cheap cars, and 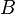 is the set of all American cars, then
is the set of all American cars, then  is the set of all cars that are either cheap, or American, or both. It does not include expensive cars that are not from America.
is the set of all cars that are either cheap, or American, or both. It does not include expensive cars that are not from America.
Complements: What's Left Over
"Complement" can mean two slightly different things in set theory.
- The complement of
 is the universe
is the universe  without any of the elements of
without any of the elements of  .
.
We write this as 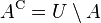 . Example: If
. Example: If 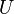 is the set of all cars, and
is the set of all cars, and  is the set of all cheap cars, then
is the set of all cheap cars, then  C is the set of all expensive cars.
C is the set of all expensive cars.
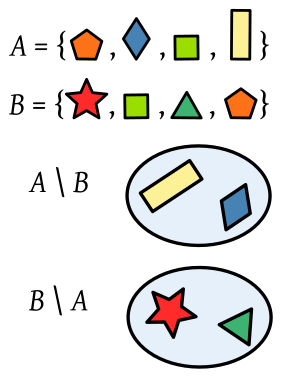
- The set difference of
 and
and 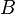 is the set
is the set 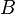 without any of the elements of
without any of the elements of  .
.
We write this as 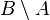 . It's also called the relative complement of
. It's also called the relative complement of  in
in 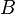 . Example: If
. Example: If  is the set of all cheap cars, and
is the set of all cheap cars, and 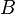 is the set of all American cars, then
is the set of all American cars, then 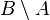 is the set of all expensive American cars.
is the set of all expensive American cars.
If you switch the sets in a set difference, the result changes. For example, 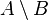 would be the set of all cheap cars that are not made in America.
would be the set of all cheap cars that are not made in America.
How to Write About Sets
Most mathematicians use uppercase italic letters for sets (like  ,
, 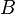 ,
, 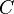 ). The elements inside the sets are usually written with lowercase letters.
). The elements inside the sets are usually written with lowercase letters.
One way to show a set is by listing its members. You separate them with commas and put them inside curly braces. For example:
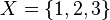 is a set with members 1, 2, and 3.
is a set with members 1, 2, and 3.
Another way is called "set-builder notation." This describes what is true about the members of the set:
- {x | x is a natural number & x < 4}.
This reads: "the set of all x such that x is a natural number and x is less than four." The symbol "|" means "such that."
The empty set can be written as 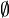 ,
, 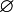 , or
, or 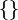 .
.
When an object a is a member of set  , it is written as:
, it is written as:
- a ∈ A.
This reads: "a is a member of  ."
."
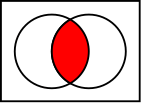
Visualizing Sets: Venn Diagrams
To help understand how sets work, mathematicians use Venn diagrams. These diagrams use circles to show individual sets. The universe (all things being considered) is shown as a rectangle around the circles. The results of set operations are shown by coloring certain areas. In the picture, the left circle is set  and the right circle is set
and the right circle is set 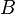 . The colored part shows their intersection.
. The colored part shows their intersection.
Important Special Sets
Some sets are used very often in mathematics. They even have special symbols. Many of these special sets are written using a special bold font called blackboard bold.
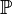 : This is the set of all prime numbers (numbers greater than 1 that can only be divided by 1 and themselves, like 2, 3, 5, 7...).
: This is the set of all prime numbers (numbers greater than 1 that can only be divided by 1 and themselves, like 2, 3, 5, 7...).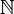 : This is the set of all natural numbers. These are the numbers you use for counting: {1, 2, 3, ...}. Sometimes, it includes 0: {0, 1, 2, 3, ...}.
: This is the set of all natural numbers. These are the numbers you use for counting: {1, 2, 3, ...}. Sometimes, it includes 0: {0, 1, 2, 3, ...}.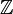 : This is the set of all integers (whole numbers, including positive, negative, and zero): {..., -2, -1, 0, 1, 2, ...}.
: This is the set of all integers (whole numbers, including positive, negative, and zero): {..., -2, -1, 0, 1, 2, ...}.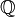 : This is the set of all rational numbers. These are numbers that can be written as a fraction
: This is the set of all rational numbers. These are numbers that can be written as a fraction 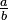 , where a and b are integers and b is not zero. For example,
, where a and b are integers and b is not zero. For example, 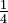 and
and 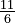 are rational numbers. All integers are rational because you can write any integer a as
are rational numbers. All integers are rational because you can write any integer a as 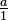 .
. : This is the set of all real numbers. This includes all rational numbers, plus irrational numbers (numbers that cannot be written as fractions, like
: This is the set of all real numbers. This includes all rational numbers, plus irrational numbers (numbers that cannot be written as fractions, like 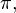
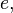 and √2).
and √2).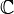 : This is the set of all complex numbers.
: This is the set of all complex numbers.
Each of these sets has an infinite number of elements. They also fit inside each other like Russian dolls: 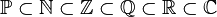 .
.
Fun with Paradoxes: The Barber Problem
The mathematician Bertrand Russell found some tricky problems with how sets were first defined. One famous problem is called Russell's paradox. A simpler version, which is easier to understand, is called the Barber paradox.
The Barber Paradox
Imagine a small town with a barber. In this town, all the men either shave themselves, or they go to the barber shop to be shaved by the barber.
The barber has a rule: "The barber shaves all men who do not shave themselves. He only shaves those men."
Now, think about the barber himself: Who shaves the barber?
- If the barber shaves himself, then according to his own rule, he cannot be the barber (because a barber only shaves those who do not shave themselves).
- If the barber does not shave himself, then he falls into the group of men who do not shave themselves. According to his rule, he must shave himself.
This creates a puzzle! It shows how careful mathematicians need to be when defining things like sets.
Related pages
The following books explore sets in more detail:
- Halmos, Paul R., Naive Set Theory, Princeton, N.J.: Van Nostrand (1960) ISBN: 0-387-90092-6
- Stoll, Robert R., Set Theory and Logic, Mineola, N.Y.: Dover Publications (1979) ISBN: 0-486-63829-4
- Allenby, R.B.J.T, Rings, Fields and Groups, Leeds, England: Butterworth Heinemann (1991) ISBN: 0-340-54440-6
See also
 In Spanish: Set para niños
In Spanish: Set para niños