Georg Cantor facts for kids

Kids Encyclopedia Facts

Quick facts for kids Georg Cantor
Cantor, c. 1910
Born	Georg Ferdinand Ludwig Philipp Cantor (1845-03-03)March 3, 1845 Saint Petersburg, Russian Empire
Died	January 6, 1918(1918-01-06) (aged 72) Halle, Province of Saxony, German Empire
Nationality	German
Alma mater	Swiss Federal Polytechnic University of Berlin
Known for	Set theory
Spouse(s)	Vally Guttmann (m. 1874)
Awards	Sylvester Medal (1904)
Scientific career
Fields	Mathematics
Institutions	University of Halle
Thesis	De aequationibus secundi gradus indeterminatis (1867)
Doctoral advisor	Ernst Kummer Karl Weierstrass

Georg Cantor (born March 3, 1845 – died January 6, 1918) was a German mathematician. He is famous for creating set theory. This is a very important part of modern mathematics.

Cantor showed how to compare the "sizes" of different groups of numbers. He proved that some infinite groups are bigger than others. This idea was new and surprising to many people. He also defined special numbers called cardinal and ordinal numbers. These numbers help us understand infinity better.

At first, many mathematicians did not like Cantor's ideas. They found his theories about different infinities hard to believe. Some even thought his work was wrong. But over time, his ideas became widely accepted. Today, set theory is a basic tool in mathematics.

Georg Cantor's Life
Cantor's Big Ideas in Math
Images for kids
See also

Georg Cantor's Life

Early Life and Education

Cantor, around 1870

Georg Cantor was born in 1845 in Saint Petersburg, Russia. He lived there until he was eleven years old. He was the oldest of six children. His family moved to Germany in 1856 because his father was ill. They hoped for milder winters there.

Cantor was a very talented student. He was especially good at mathematics. In 1862, he started studying at the Swiss Federal Polytechnic in Zurich. After his father passed away in 1863, Cantor moved to the University of Berlin. There, he learned from famous mathematicians. He earned his doctoral degree in 1867.

Becoming a Professor

After finishing his studies, Cantor taught for a short time in a girls' school. Then, he got a job at the University of Halle. He stayed there for his entire career. He became a full professor in 1879 when he was 34. This was a great achievement.

In 1874, Cantor married Vally Guttmann. They had six children together. Cantor could support his family thanks to money he inherited from his father. He often discussed math with his friend Richard Dedekind.

Challenges and Recognition

Cantor wanted to work at a more famous university, like the University of Berlin. But his ideas faced a lot of opposition. A powerful mathematician named Leopold Kronecker strongly disagreed with Cantor's work. Kronecker believed that only numbers that could be built in a finite number of steps were real. He thought Cantor's ideas about different infinities were wrong.

Kronecker's opposition made it hard for Cantor to get a job in Berlin. Cantor felt that Kronecker was preventing him from moving. This criticism affected Cantor deeply. He started to struggle with depression in 1884.

Despite the challenges, Cantor continued his important work. He developed his famous "diagonal argument" in 1891. This argument showed that there are different sizes of infinity. He also helped create the German Mathematical Society in 1889. He was chosen as its first president.

In 1904, the Royal Society gave Cantor the Sylvester Medal. This was a very high honor for his work in mathematics. Another famous mathematician, David Hilbert, praised Cantor's work. He said, "No one shall expel us from the paradise that Cantor has created."

Later Years and Passing

Cantor continued to struggle with his mental health throughout his later life. He was hospitalized several times. In 1899, his youngest son, Rudolph, died suddenly. This tragedy made Cantor lose much of his passion for mathematics.

In 1904, a paper presented at a math conference upset him greatly. It tried to prove that his set theory was false. Even though the proof was quickly shown to be wrong, Cantor was shaken. He continued to have periods of depression.

Cantor retired in 1913. He faced poverty and poor health during World War I. He passed away on January 6, 1918, in a sanatorium.

Cantor's Big Ideas in Math

Cantor's work from 1874 to 1884 started the field of set theory. Before him, people thought of sets as simple groups of things. They didn't realize that set theory could be so complex. Cantor showed that there are many different "sizes" of infinite sets. This made set theory a very important area of study.

Set theory is now a basic part of modern mathematics. It helps explain ideas about numbers and functions. It provides a common language for many areas of math.

Comparing Infinite Sizes

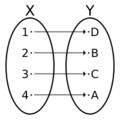
Cantor proved that the set of real numbers is "larger" than the set of natural numbers. This was the first time anyone showed that infinite sets could have different sizes. He used the idea of a one-to-one correspondence. This means pairing up each item in one set with exactly one item in another.

He used this idea to define finite and infinite sets. He also divided infinite sets into two types:

Countable sets: These can be put into a one-to-one correspondence with the natural numbers.
Uncountable sets: These are "bigger" than the natural numbers. They cannot be counted in the same way.

The Power of Sets

Cantor introduced the idea of a power set. This is the set of all possible subsets of a given set. For example, if you have a set {A, B}, its power set would be {{}, {A}, {B}, {A, B}}.

He proved that the power set of any set is always strictly larger than the original set. This is true even for infinite sets. This important result is known as Cantor's theorem. It showed that there is an endless hierarchy of infinities.

Cantor also created a system for working with infinite numbers. He called them cardinals and ordinals. He used the Hebrew letter 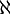$\aleph$ (aleph) for cardinal numbers. He used the Greek letter ω (omega) for ordinal numbers. These symbols are still used today.

The Continuum Hypothesis

Cantor also came up with the Continuum hypothesis. This idea suggests that there is no set whose size is between the natural numbers and the real numbers. In simpler terms, it asks if the real numbers are the "next biggest" infinity after the natural numbers.

Cantor believed this idea was true. He tried for many years to prove it, but he couldn't. Later mathematicians showed why this was so difficult. In fact, the continuum hypothesis cannot be proven or disproven using standard set theory rules.

Understanding Paradoxes

Cantor realized that there were different types of infinite collections. Some could be treated as "sets" (consistent multiplicities). Others were "too big" to be sets (inconsistent multiplicities). This helped him avoid certain paradoxes (logical contradictions).

Later, other mathematicians like Bertrand Russell found paradoxes in set theory. These paradoxes showed that some ways of thinking about sets could lead to contradictions. To fix this, new systems of set theory were developed. These systems, like Zermelo–Fraenkel set theory, set rules for what counts as a set. This helped make set theory a solid foundation for mathematics.

Images for kids

Passage of Georg Cantor's article with his set definition
An illustration of Cantor's diagonal argument for the existence of uncountable sets. The sequence at the bottom cannot occur anywhere in the infinite list of sequences above.
A bijective function
The title on the memorial plaque (in Russian): "In this building was born and lived from 1845 till 1854 the great mathematician and creator of set theory Georg Cantor", Vasilievsky Island, Saint-Petersburg.