kids encyclopedia robot

Cantor's diagonal argument facts for kids

Kids Encyclopedia Facts

Cantor's diagonal argument is a clever math trick used to compare the "size" of different infinite sets. It helps us understand if two endless groups of numbers or items have the same number of things in them.

A mathematician named Georg Cantor came up with this idea. He published his first proof of this argument in 1890.

Cantor said that two sets have the same "size" (mathematicians call this cardinality) if you can match up each item from the first set with exactly one item from the second set, and vice versa. This is easy to see with finite sets (sets with a limited number of items). But it's much harder to imagine with infinite sets!

Comparing Natural Numbers and Fractions

Let's look at one of Cantor's first examples. He wanted to show that the set of natural numbers (1, 2, 3, 4, ...) and the set of positive fractions (like 1/2, 3/4, 5/1) actually have the same "size."

First, imagine writing out all the positive fractions in a grid, like this: \begin{array}{cccccccccc} \tfrac 11 & & \tfrac 12 & & \tfrac 13 & & \tfrac 14 & & \tfrac 15 & \cdots \\ & & & & & & & & & \\ \tfrac 21 & & \tfrac 22 & & \tfrac 23 & & \tfrac 24 & & \tfrac 25 & \cdots \\ & & & & & & & & & \\ \tfrac 31 & & \tfrac 32 & & \tfrac 33 & & \tfrac 34 & & \tfrac 35 & \cdots \\ & & & & & & & & & \\ \tfrac 41 & & \tfrac 42 & & \tfrac 43 & & \tfrac 44 & & \tfrac 45 & \cdots \\ & & & & & & & & & \\ \tfrac 51 & & \tfrac 52 & & \tfrac 53 & & \tfrac 54 & & \tfrac 55 & \cdots \\ \vdots & & \vdots & & \vdots & & \vdots & & \vdots & \\ \end{array}

Now, to count them, Cantor used a special path. He went diagonally through the grid. He skipped any fractions that could be simplified (like 2/2, which is 1/1). This way, he could match each natural number to a unique fraction:

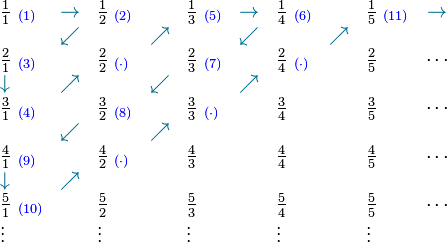
\begin{array}{lclclclclc} \tfrac 11\ _{\color{Blue} (1)} & {\color{MidnightBlue}\rightarrow} & \tfrac 12\ _{\color{Blue} (2)} & & \tfrac 13\ _{\color{Blue} (5)} & {\color{MidnightBlue}\rightarrow} & \tfrac 14\ _{\color{Blue} (6)} & & \tfrac 15\ _{\color{Blue} (11)} & {\color{MidnightBlue}\rightarrow} \\ & {\color{MidnightBlue}\swarrow} & & {\color{MidnightBlue}\nearrow} & & {\color{MidnightBlue}\swarrow} & & {\color{MidnightBlue}\nearrow} & & \\ \tfrac 21\ _{\color{Blue} (3)} & & \tfrac 22\ _{\color{Blue} (\cdot)} & & \tfrac 23\ _{\color{Blue} (7)} & & \tfrac 24\ _{\color{Blue} (\cdot)} & & \tfrac 25 & \cdots \\ {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\nearrow} & & {\color{MidnightBlue}\swarrow} & & {\color{MidnightBlue}\nearrow} & & & & \\ \tfrac 31\ _{\color{Blue} (4)} & & \tfrac 32\ _{\color{Blue} (8)} & & \tfrac 33\ _{\color{Blue} (\cdot)} & & \tfrac 34 & & \tfrac 35 & \cdots \\ & {\color{MidnightBlue}\swarrow} & & {\color{MidnightBlue}\nearrow} & & & & & & \\ \tfrac 41\ _{\color{Blue} (9)} & & \tfrac 42\ _{\color{Blue} (\cdot)} & & \tfrac 43 & & \tfrac 44 & & \tfrac 45 & \cdots \\ {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\nearrow} & & & & & & & & \\ \tfrac 51\ _{\color{Blue} (10)} & & \tfrac 52 & & \tfrac 53 & & \tfrac 54 & & \tfrac 55 & \cdots \\ \vdots & & \vdots & & \vdots & & \vdots & & \vdots & \\ \end{array}

This method creates a perfect match, or a bijection, between the natural numbers and the positive fractions. \begin{array}{cccccccccccccccc} {\color{Blue} 1} & {\color{Blue} 2} & {\color{Blue} 3} & {\color{Blue} 4} & {\color{Blue} 5} & {\color{Blue} 6} & {\color{Blue} 7} & {\color{Blue} 8} & {\color{Blue} 9} & {\color{Blue} 10} & {\color{Blue} 11} & {\color{Blue} \cdots} \\[3pt] {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} \\[3pt] 1 & \tfrac 12 & 2 & 3 & \tfrac 13 & \tfrac 14 & \tfrac 23 & \tfrac 32 & 4 & 5 & \tfrac 15 & \cdots \\ \end{array}

To include all fractions (positive, negative, and zero), you can add 0 and then each fraction's negative value. \begin{array}{cccccccccccccccc} {\color{Blue} 1} & {\color{Blue} 2} & {\color{Blue} 3} & {\color{Blue} 4} & {\color{Blue} 5} & {\color{Blue} 6} & {\color{Blue} 7} & {\color{Blue} 8} & {\color{Blue} 9} & {\color{Blue} 10} & {\color{Blue} 11} & {\color{Blue} 12} & {\color{Blue} 13} & {\color{Blue} 14} & {\color{Blue} 15} & {\color{Blue} \cdots} \\[3pt] {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} & {\color{MidnightBlue}\downarrow} \\[3pt] 0 & 1 & -1 & \tfrac 12 & -\tfrac 12 & 2 & -2 & 3 & -3 & \tfrac 13 & -\tfrac 13 & \tfrac 14 & -\tfrac 14 & \tfrac 23 & -\tfrac 23 & \cdots \\ \end{array}

This shows that the set of all fractions has the same "size" as the set of natural numbers. Sets that can be matched up with the natural numbers are called countable. This means we can list them out, even if the list is endless.

Infinite sets can sometimes behave in surprising ways. For example, Hilbert's paradox of the Grand Hotel shows how an infinite hotel can always fit more guests, even when it's full!

Real Numbers are Different

Cantor then used a similar but even more powerful argument to show something amazing: the set of real numbers is bigger than the set of natural numbers. This means there are more real numbers than natural numbers.

Real numbers include all numbers on a number line, like fractions, whole numbers, and numbers like pi (π) or the square root of 2.

In 1891, Cantor looked at infinite lists (or sequences) made up of only 0s and 1s. For example:

  • (0, 0, 0, 0, 0, 0, 0, ...)
  • (1, 1, 1, 1, 1, 1, 1, ...)
  • (0, 1, 0, 1, 0, 1, 0, ...)

He proved that no matter how you try to list all these sequences, you will always miss at least one.

Here's how his argument works: Imagine you try to make a list of all possible infinite sequences of 0s and 1s. Let's say your list looks like this:

s1 = (0, 0, 0, 0, 0, 0, 0, ...)
s2 = (1, 1, 1, 1, 1, 1, 1, ...)
s3 = (0, 1, 0, 1, 0, 1, 0, ...)
s4 = (1, 0, 1, 0, 1, 0, 1, ...)
s5 = (1, 1, 0, 1, 0, 1, 1, ...)
s6 = (0, 0, 1, 1, 0, 1, 1, ...)
s7 = (1, 0, 0, 0, 1, 0, 0, ...)
...

Now, Cantor created a new sequence, let's call it s, that is guaranteed not to be on your list. He did this by looking at the "diagonal" of your list:

  • For the first digit of s, he took the first digit of s1 and flipped it (0 becomes 1, 1 becomes 0).
  • For the second digit of s, he took the second digit of s2 and flipped it.
  • For the third digit of s, he took the third digit of s3 and flipped it.
  • And so on for every digit.

Let's see what s would be for our example list:

s1 = (0, 0, 0, 0, 0, 0, 0, ...)
s2 = (1, 1, 1, 1, 1, 1, 1, ...)
s3 = (0, 1, 0, 1, 0, 1, 0, ...)
s4 = (1, 0, 1, 0, 1, 0, 1, ...)
s5 = (1, 1, 0, 1, 0, 1, 1, ...)
s6 = (0, 0, 1, 1, 0, 1, 1, ...)
s7 = (1, 0, 0, 0, 1, 0, 0, ...)
...
s = (1, 0, 1, 1, 1, 0, 1, ...)

Because s is different from s1 in its first digit, different from s2 in its second digit, and so on, it cannot be any of the sequences on your list!

This means that no matter how you try to list all infinite sequences of 0s and 1s, you will always miss at least one. This proves that the set of these sequences is "uncountable." Since real numbers can be represented by such sequences, it also means the set of real numbers is uncountable. It's a bigger infinity!

See also

A robot thinking about numbers.

kids search engine
All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Cantor's diagonal argument Facts for Kids. Kiddle Encyclopedia.