Cardinality facts for kids
The cardinality of a set is a way to describe how many items are in that set. Think of it like counting how many toys are in a box. For example, if you have a set of numbers like A = {2, 4, 6}, it has 3 items. So, the cardinality of set A is 3. We can write this as 
.
Two sets have the same cardinality if they have the exact same number of items. This means you can pair up every item in one set with an item in the other set, with no items left over. If set A has fewer items than set B, or the same number, we say the cardinality of A is less than or equal to the cardinality of B. This means you can fit all the items from set A into set B without using any item in B more than once.
Cardinality helps us understand the "size" of a set, even when sets are very large or even infinite.
Counting Items in Finite Sets
When a set has a specific, countable number of items, we call it a finite set. The cardinality of a finite set is always a natural number (like 0, 1, 2, 3, and so on).
The smallest possible cardinality is 0. This belongs to the empty set, which is a set with no items at all. If a set has n items, you can always make a slightly larger set with n+1 items by adding just one more thing. This means there's no biggest finite number of items a set can have!
Understanding Infinite Sets
Sometimes, a set has so many items that you can't count them all. These are called infinite sets.
Some infinite sets can still be "counted" in a special way. If you can list all the items in an infinite set without missing any, we call it a countable set. This means you can match each item in the set with a natural number (1st, 2nd, 3rd, and so on). Examples include the set of all integers (whole numbers, positive and negative) and the set of all rational numbers (fractions). The cardinality of these sets is called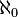 
(pronounced "aleph null" or "aleph zero").
However, some infinite sets are so big that they are uncountable. This means you can't possibly list all their items, even if you tried forever. The set of all real numbers (which includes all numbers on the number line, like decimals and numbers like pi) is an example of an uncountable set. No matter how you try to list them, you can always find a real number that's not on your list. The cardinality of the real numbers is called 
, which stands for the "cardinality of the continuum."
Related Ideas
- Bijection
- Cardinal number
- Cantor's diagonal argument
- Cantor's theorem
- Continuum hypothesis
- Injective function
See also
In Spanish: Cardinalidad para niños
